| Prominence-Isolation Concepts * |
|
There are precious few completely objective mountain metrics. Among these, topographic prominence and isolation measure generate useful peak lists of interest to climbers. Prominence rewards mountains with large vertical relief; isolation measure those geographically remote from higher terrain.
Various "flavors" of isolation measure exist, including, most commonly, the distance to a higher summit. Isolation is also definable as distance to higher ground even when the latter is not a mountaintop; distance to a more prominent peak; and even distance to a more isolated peak. This note, and the associated table and graph, defines isolation as distance to a higher summit. The summit, in theory, should have any prominence. In practice, however, summits typically must have at least 300 feet of prominence to qualify.
Three Regions: Great Britain, Continental United States, World
Given that prominence alone and isolation alone produce valuable peak lists,
it is instructive to consider how combinations of these two metrics fare insofar as
their ability to generate lists of desirable mountains for the peakbagger.
The most obvious and simplest combination is multiplication of prominence by isolation,
the product having units of length2. The product itself is not too meaningful,
as in particular prominence is typically reported in meters or feet while isolation is
typically in kilometers or statute miles. Henceforth this product is termed "P-I measure".
Three regions are studied with different sizes: Great Britain; the forty-eight state contiguous United States
(henceforth, "CONUS" for "CONtinental United States"); and the entire world.
Later, the differing areas allow for studying the scale-dependence of prominence and isolation statistics.
Great Britain
Robert Woodall has determined the United Kingdom summits with largest P-I measure.1
The present work restricts consideration to summits in Great Britain, excluding North Ireland
and the Isle of Man. The resulting 50 summit list
has a cutoff P*I measure of 15.3 km2; and includes six summits that are not on either
the Great Britain top 50 list by prominence nor on the Great Britain top 50 list by isolation.
A graph displays prominences and isolations of British summits
with logarithmic axes. There are a total of 93 summits represented - including 37 summits that are on the British
top 50 by prominence list only; 37 summits on the top 50 by isolation list only;
13 summits on both of these lists; and the six summits on the British top 50 list by
P-I measure and yet on neither original list. There are 87 summits on at least one of the two
top 50 lists by prominence and/or by isolation.
The top 50 by prominence cutoff is 706 meters; the top 50 by isolation cutoff is 37 kilometers.
Ben Nevis dominates the graph, having the top-ranked prominence and isolation.
Robert Woodall has produced a map displaying the most prominent and most isolated summits
throughout Great Britain
and a second map for the entire United Kingdom.
With these maps and his P-I measure results one reaches any number of interesting observations
for the British peakbagger. These are left as exercises.
Continental United States
Ryan Richardson tabulates peaks
in the 48 contiguous United States by P-I measure. The list is an excellent collection of peaks
insofar as containing prominent summits (San Jacinto Peak, California),
isolated summits (Magazine Mountain, Arkansas), and summits with a good amount of both measures
(Mount Mitchell, North Carolina).
A graph displays prominences and isolations of CONUS summits
with logarithmic axes. There are a total of 83 summits represented - including 29 summits that are on the CONUS
top 50 by prominence list only; 29 summits on the top 50 by isolation list only;
21 summits on both of these lists; and four summits on the CONUS top 50 list by
P-I measure and yet on neither original list. There are 79 summits on at least one of the two
top 50 lists by prominence and/or by isolation.
The top 50 by prominence cutoff ("America's Fifty Finest") is 5,220 feet;
the top 50 by isolation cutoff is 89.3 statute miles.
Further discussion of this graph is included below in the section on prominence and isolation character.
World
The author has determined the world top 50 summits by P-I measure;
the 19 summits of Earth's Fifty Finest list that do not rank in the top 50 by P-I measure; and
the 10 summits of the top 50 by isolation list that do not rank in the top 50 by P-I measure.
The collective data allows for several observations.
A graph displays prominences and isolations of world summits with logarithmic axes. There are a total of 81 summits represented - including 29 summits that are on the Earth Fifty Finest list only; 29 summits on the top 50 by isolation list only; 21 summits on both of these lists; and two summits on the world top 50 list by P-I measure and yet on neither original list. There are 79 summits on at least one of the two top 50 lists by prominence and/or by isolation.
These sublists are available for inspection.
The graph is a noteworthy portayal of objectively impressive summits - a single glance allowing assessment of their relative stature (prominence) and isolation. The Earth Fifty Finest cutoff is 11,550 feet; the world top 50 by isolation cutoff is 860 miles.
Prominence and Isolation Character
One may quantify the extent to which prominence and isolation
individually contribute to their product P-I measure.
Various formulations are possible, and have been employed in detailed calculations by the author.
Theoretically both prominence and isolation are power-law distributed, meaning that the numbers of peaks,
in either metric, are distributed according to a power law function:
On Earth both prominence and isolation density are roughly power-law distributed.
Thus quantification of how much prominence and isolation contribute to P-I measure is best
realized using the logarithms of prominence and isolation.
We define the prominence character Since the logarithm of zero is undefined, zeroes of the prominence and isolation scales
are defined respectively by the least prominent and least isolated peaks on a list.
The most prominent and most isolated peaks define unit character. Then, for consistency,
arithmetic scales are similarly defined.
One could define absolute prominence and isolation scales. However one then has to select
arbitrary minimum and maximum values. In principle this is possible by amassing a
global database of peaks with their prominence and isolation values, and choosing the maximum
prominence and isolation using Mount Everest. However the minimum prominence and isolation
would be highly dependent on the smallest bump's identity. Given these pitfalls, the present work
simply defaults to a list-dependent set of prominence and isolation characters.
To compute character values several prescriptions are used -
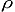(f) = A f -
.
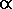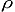Here, prominence p or isolation r is denoted by f; (f)
is the density of prominence or isolation values
(in meters-1 or kilometers-1);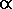
is the power law exponent; and A is a constant.
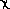(p) of a mountain
as the fraction of its P-I measure contributed by prominence in a logarithmic or arithmetic sense.
Isolation character is then simply
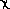(r) = 1 - 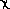(p).2
as proposed by Edward Earl. No normalization is required.
/2 radians.
Great Britain
The prominence and isolation characters of British summits
are tabulated using several of these prescriptions. All 87 summits that are on at least one
of the top 50 by prominence or by isolation lists are included. Some observations regarding the
limiting character values follow.
Hence it defines the isolation scale's bottom.
Its prominence character is 1.0; its isolation character is 0.0 .
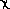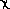(p) + (r) = 1.000)
then yields prominence and isolation characters of 0.5000 each.
Further analysis of prominence and isolation character is left as an exercise.
Continental United States
Pairs of ( The arithmetic and logarithmic prominence and isolation characters using an arctangent function
are presented in this text file.
Here, peaks are separated into three tables according to their presence on either or both
of the original peak lists; and, within each table, are ranked in descending order
of logarithmic prominence character For completeness, the entire set of raw prominence and isolation characters are presented in this
text file for all six combinations
of scaling function (arithmetic, logarithmic) and character definitions (simple, arctangent, direction cosine).
The arctangent results allow
several observations (results for other character definitions are qualitatively similar).
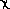(p), 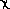(r))
are calculated for a 79-peak list defined by the union of the 50 most prominent summits in the
CONUS and the 50 most isolated summits for that region.
As noted previously, the list contains 21 peaks on both original lists; 29 prominent peaks without sufficient
isolation to make the 50 most isolated peak list; and 29 isolated peaks without sufficient
prominence to make the 50 most prominent peak list. The prominence cutoff of 5,220 feet allows
inclusion of Mount Cleveland, Montana (number 50) but not Arc Dome, Nevada (number 51).
The isolation cutoff of 89.3 statute miles allows for including Baldy South of New Mexico
but not the Clay County, Florida highpoint.
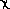(p).
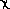(p) > 0.75) and peaks with large isolation and small prominence
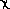((r) > 0.75) have small P-I measure.
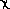(p) = 0.7387 (Mount Olympus, Washington) to
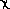(p) = 0.4557 (Mount Mitchell, North Carolina).
World
The prominence and isolation
characters of world summits
are tabulated using several prescriptions. All 79 summits that are on at least one
of the top 50 by prominence or by isolation lists are included. Separate tabulations are provided
for peaks only on Earth's Fifty Finest (29 peaks); only in the top 50 by isolation (29 peaks);
and on both of these lists (21 peaks). Within each table peaks are listed in descending prominence character
using the logarithmic arctangent function.
Some observations regarding the limiting character values follow.
Hence it defines the isolation scale's bottom.
Its prominence character is 1.0; its isolation character is 0.0 .
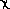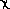(p) + (r) = 1.000)
then yields prominence and isolation characters of 0.5000 each.
Peaks with small isolation distance, on the order of 75-120 miles, have nearly complete prominence character. Examples include Mount Erebus (0.9539), Kangchenjunga (0.9597), the Finisterre Range Highpoint (0.9104), and Nanga Parbat (0.8798). All of these are Earth Fifty Finest summits.
Peaks with the largest prominences and isolation distances have both the largest P-I measure and characters that evenly balance prominence and isolation. Examples include Mount Everest (0.5000), Aconcagua (0.5205), Mount McKinley (0.5518), and Kilimanjaro (0.5654).
Oceanic island highpoints with large isolation distance and relatively small prominence have more isolation than prominence character.
Generalization of P-I Measure
P-I measure rewards prominence and isolation in equal measure. It is a special case
of the prescription f(p,r) = px r1-x, where 0.0 ≤ x ≤ 1.0;
p represents prominence, and r isolation. The choice x = 1.0 yields (pure) prominence;
the choice x = 0.0 yields (pure) isolation; and x = 0.5 yields P-I measure.
It is instructive to consider how intermediate values of x change the peaks represented
on a top N list. We have already seen how x = 0.5 yields peaks on neither
the N = 50 lists generated by x = 0.0 and x = 1.0: six for Great Britain, four in the CONUS,
and two for the entire world.
The situation is best portrayed graphically by any of the log-log
isolation - prominence scatterplots
used above to portray the distribution of peaks along those two dimensions for various regions.
These graphs encapsulate many of the concepts outlined here,
and should be thoroughly studied by the reader.
A horizontal line represents the prominence cutoff of the top 50 by prominence list.
A vertical line represents the isolation cutoff of the top 50 by isolation list.
Diagonal lines represent the P-I measure cutoff for intermediate choices of x.
For x = 0.5 a 45° line from upper left (large prominence, low isolation) to
lower right (low prominence, large isolation) separates peaks on the P-I measure list
to the upper right from those with insufficient P-I measure.
Peaks are represented on the P-I measure list yet not on either "pure" list
when they lie to the upper right of the corresponding diagonal.
Choices of x besides 0.5 will result in different diagonals; and, with them,
a methodical progression of peaks being included, and excluded, from the corresponding list.
Examination of data points above the horizontal prominence cutoff reveals a positive
correlation between prominence and isolation. This is expected, since the most isolated peaks
are the highest in their respective, multi-state regions - and, with that, also have large prominence.
Prominence and isolation distance are positively correlated for Earth's Fifty Finest summits -
and, as N = 50 is arbitrary, this correlation must exist in general.
Prominence and Isolation Scaling Properties
By re-scaling one isolation-prominence graph it can be superimposed atop another graph.
Several re-scaling prescriptions are available -
and similarly for the prominence-axis.
All of these formulations have been implemented as code.
Superimposing the Great Britain isolation-prominence data upon the CONUS data results in this rescaled graph. The first prescription is used, i.e. re-scaling the Great Britain isolation cutoff of 37 kilometers to the CONUS cutoff of 89.3 miles; and similarly for the prominence axis.
Superimposing the world isolation-prominence data upon the CONUS data results in this rescaled graph. The first prescription is used, i.e. re-scaling the world isolation cutoff of 860 miles to the CONUS cutoff of 89.3 miles; and similarly for the prominence axis.
The superficial resemblance of the CONUS and superimposed data is remarkable. The superimposed datapoints must, owing to the re-scaling prescription, all lie in the three rectangles defined as the set of points with at least one coordinate at least equal to the CONUS isolation or prominence cutoff. Even accounting for this fact (which makes the superimposed data appear more closely related to the CONUS data than warranted); one is still left with distributions of superimposed points, be they for the Great Britain or the world data, that lie atop the CONUS datapoints to extents far greater than would points randomly distributed in either log-log isolation-prominence space or in isolation-prominence space alone.
The key concept is scale invariance, a property owned by fractal objects.
Fractals appear similar on all length scales examined. In theory the density of prominent summits,
were terrain to be fractal in nature, would scale according to a perfect power-law function,
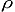(p) = A p -;
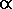and similarly for isolation; both with the choice 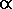= 3.0 .
On Earth both prominence and isolation density are roughly power-law distributed.
It is the approach of real-world data to perfect power-law prominence and isolation distributions,
both with 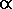= 3.0, that accounts for the visual similarity
of the Great Britain and world data when superimposed on the CONUS data.
These concepts are currently under study in an effort to better quantify
(and possibly explain) the observed distributions on datapoints in (log r, log p) space.
1Robert Woodall's
entire list is available as a Microsoft Excel file.
The present work does not incorporate
North Ireland and the Isle of Man
because these are separate topographic entities. Only summits in Great Britain are considered.
2 "Remoteness" has been suggested as an alternative to "isolation".
The latter has, at least in English,
the connotation of "banished" or "secluded" -
inappropriate concepts in the present context.
Furthermore, "remoteness"
has the advantage of being abbrevated by "r", the standard symbol for radius in geometry.
3Prominences and isolations of these peaks are found at the bottom of this text file.
4The isolation of Mount Everest, as with its prominence, is undefined.
Some value had to be provided - and Earth's circumference is used here.
