|
The Determination of Pressure Altitude and Implications for High Altitude Physiology
© 2006 Adam Helman, Ph.D.1, Jared Workman, Ph.D., and John Sype, M.D.2 |
1 Address all correspondence to Dr. Helman
at helman@san.rr.com .
2
The Cardiac Center at Creighton University
Creighton University School of Medicine
3006 Webster Street
Omaha, Nebraska 68131
Pressure altitude is the single most important variable in the physiology of high altitude mountaineering. The variations of pressure altitude with changes in true altitude, ambient temperature, latitude, and other meteorological variables are explored. Temperature shifts have moderately large effects upon pressure altitude; cold bringing a rise in pressure altitude (i.e. diminished pressure), and conversely with heat.
Pressure altitude is effected by latitude-dependent variations in the acceleration due to gravity at sea level. The contribution is sufficiently minor to be neglected in the climbing arena.
Pressure altitude is effected by global atmospheric circulation patterns as generated by differential heating and Coriolis forces. In addition, variations in pressure altitude arise from regional weather patterns through temperature shifts that alter the atmospheric scale height. This pressure altitude variability is treated empirically using pressure data extrapolated from observation at lower altitude.
Application is made to the air pressure at Mount McKinley, Aconcagua, and Mount Everest - the latter representing high Asian summits. The Mount McKinley summit pressure during the May and June climbing season is on average encountered 300 meters (1,000 feet) higher on Aconcagua at 6,500 meters (21,350 feet); and 400 meters (1,300 feet) higher on Mount Everest at 6,600 meters (21,650 feet), each mountain being considered during its respective climbing season.
These true altitude differences for matching summit pressure are not due to colder than standard temperatures at Mount McKinley. The differences arise from warmer than standard temperatures at the comparison mountains.
The implications for high altitude physiology of non-standard temperatures and pressures are discussed; with "oxygenless" ascents of Mount Everest as example.
It is common knowledge that atmospheric pressure decreases with rising altitude. Less well-known is that temperature and latitude influence this relationship with small yet quantifiable effects. The global atmospheric circulation caused by differential heating and Earth's rotation also results in moderate sea level pressure variations that shift pressure altitude. These relationships are explored.
We begin with a review of previous work on pressure altitude determination. The defining equations which specify the altitude-dependence of atmospheric pressure are then derived at two levels of approximation. A temperature and a latitude-dependence of pressure altitude result, with the latter arising from changes in the value of g, the acceleration due to gravity, with latitude.
Centripetal acceleration due to the atmosphere's co-rotation with the rocky Earth is shown to have a negligible direct effect on pressure altitude.
An empirical approach specifies in a probabilistic sense the effect of global circulation patterns on pressure altitude. Specific mountains are selected, and statistical analyses of meteorological data from nearby stations provide a seasonal description of local pressure altitude variability.
Although several types of altitude have been defined (cf Appendix A), discussion is restricted to pressure altitude as the key variable in high altitude physiology.
The pressure altitudes at Mount McKinley, Aconcagua, and Mount Everest are calculated and contrasted. These results are discussed and summarized.
The current work provides a framework for quantitating the effect of nonstandard air temperature, and air pressure, upon maximal oxygen consumption rate.
A simplified, easy-to-read version of this article is available without the detailed derivations and formulae.
The Standard Atmosphere has long been used by the aviation community and other practical applications to specify how pressure declines with true altitude. However this model was never intended to accurately predict pressure altitude under a wide range of environmental conditions.
As demonstrated in the next two sections, pressure altitude is principally determined by temperature in the air column - and this varies greatly with both location and season. Noting this, the geophysics community produced a set of atmospheric models, each being appropriate for a specific combination of latitude and calendar month.1 Here, each latitude/season pair acts as a surrogate for temperature as the true, underlying variable in the equations which determine pressure altitude.
Terris Moore considered the effect of low temperature upon barometric pressure at Earth's highest mountains in a 1968 paper addressed to the climbing community.2 Using a similar approach based on latitude as the independent variable, Dr. Moore cited United States Air Force tabulations of barometric pressure in 10° latitude ranges from 0 to 100,000 feet in 10,000 foot increments. He then interpolated to obtain equivalent pressure altitudes. Dr. Moore's results are compared and contrasted with the current work in the Discussion.
John West considered pressure altitude in a key 1996 paper addressed to the high altitude physiology community.3 He applied the latitude and seasonally-dependent geophysical models to calculate pressure altitude with high accuracy for a range of montane settings.
The key contribution Dr. West made was to realize and act upon the fact that the Standard Atmosphere is inadequate for estimating pressure altitude given a specific location and observation date. Then, he employed latitude/season pairs as the independent variable, as do the geophysical models, to accurately calculate pressure altitude.
The current work does not use latitude/season pairs as the independent variable for determining which atmospheric model is applicable to a specific montane setting. Instead, we derive the exact equations that specify how temperature of the air column determines pressure altitude; and then apply these equations to specific mountains during their optimal climbing season.
Our approach obviates use of any particular geophysical model by relying upon meteorological observations at or near the mountain of interest; the readings taken during the exact month for which pressure altitude is desired.
The current work provides a methodology for estimating the variability in pressure altitude due to weather. There results a model for assessing both the mean and variance of pressure altitude at any time and location given sufficient meteorological data.
In this section the dependence of air pressure on true altitude is derived at the simplest level of theory.
Consider an air column of unit cross-sectional area extending from the ground to infinite height. At any elevation z we have the hydrostatic equation,
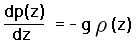 |
(1a) |
Here p(z) is the atmospheric pressure, and arises from the weight of the air parcel
above the given height; 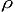 (z) is the air density; and g is the
acceleration due to gravity.
The negative sign in Equation (1) accounts for the decrease of pressure with rising height.
Equation (1) states that the contribution to pressure of a minutely short air parcel equals its
weight per unit cross-sectional area - and that air pressure is lower above the parcel than below it.
(z) is the air density; and g is the
acceleration due to gravity.
The negative sign in Equation (1) accounts for the decrease of pressure with rising height.
Equation (1) states that the contribution to pressure of a minutely short air parcel equals its
weight per unit cross-sectional area - and that air pressure is lower above the parcel than below it.
For the lower atmosphere the Ideal Gas Law
is a valid approximation,
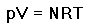 |
(2a) |
We have
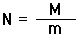 |
(3) |
where M is the total mass and m is the mean atomic mass of the gas molecules.
We also have
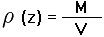 |
(4) |
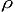 (z) is simply mass per unit volume.
(z) is simply mass per unit volume.
Substitution of Equations (3,4) into Equation (2a) yields
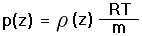 |
(2b) |
Solution of Equation (2b) for 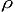 (z) and substitution
into Equation (1) yields
(z) and substitution
into Equation (1) yields
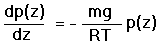 |
(1b) |
and the differential equation
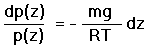 |
(5) |
Equation (5) is now integrated on the left hand side from a reference, sea level pressure p(0), to p(z); and on the right hand side from 0 to height z,
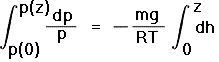 |
(6) |
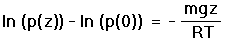 |
(7a) |
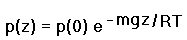 |
(7b) |
We define the atmospheric scale height H as that altitude at which the pressure has dropped to the fraction 1/e of sea level pressure (about 0.368),
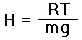 |
(8) |
In terms of H, Eq.(7b) yields
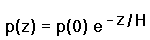 |
(7c) |
For Earth's atmosphere, H is roughly 8,000 meters (26,400 feet).4
In Equations (8) and (7c) R is a constant; while m is constant up to roughly 90-100 kilometers (55-60 miles) height. Above that altitude there is an increasing preponderance of lighter species such as hydrogen, and a consequent decline in m. These altitudes are of no concern to mountaineering.
Thereby any effects of latitude and temperature upon atmospheric pressure must arise from their effects upon the remaining variables g and T. Note that the sea level pressure p(0) does not vary with latitude.
In these derivations we have assumed g to be a constant throughout the air column's height. Sparing the details, account of diminishing g with rising altitude replaces the term gz in Equation (7b) by the approximate expression g(0)z(1 - bz). g(0) is the acceleration due to gravity at sea level in the Standard Atmosphere. b is one-half the fractional decrease in g per unit increment in altitude, equaling 1/Re where Re is Earth's radius.5
At the atmosphere's true scale height, z(1 - bz) is less than z by roughly 10 meters (33 feet).4 Thereby the pressure at height H using g(0)z(1 - bz) exceeds that predicted using the factor gz by an amount realizable using 10 meters less true altitude - a small amount. Further, as the correction term -bz2 scales with the square of the altitude, it is smaller still for most altitudes of mountaineering interest, i.e. less than the atmospheric scale height.
To first order, this minor, positive pressure correction occurs at all mountains equally for a given true altitude. Upon comparison of pressure altitudes between mountains the effect cancels. We are thus justified in neglecting changes in g with true altitude.
In the last section we assumed the absolute temperature T is fixed throughout the air column. A more accurate description has the temperature decline linearly with true altitude for elevations restricted to the troposphere. The rate of temperature decline is called the lapse rate and is denoted "L". In the equations below we define L to be negative-valued for a decrease in temperature with true altitude.
The lapse rate's magnitude has important consequences for the stability of air. If the lapse rate's magnitude is less than the dry adiabatic lapse rate of 9.78° C / km (5.37° F / 1,000 feet) then a rising parcel of air will eventually cool to the point that it is denser than the surrounding air, and thus cease to rise. An environmental lapse rate of 6.5° C / km (3.57° F / 1,000 feet) is considered a good overall value representative of real atmospheric conditions, and, being less than the dry adiabatic lapse rate, corresponds to stable air. When the lapse rate's sign is positive (a rise in temperature with true altitude), the air is particularly stable - a temperature inversion.
We begin with Equation (5) but with the temperature T a linear function of z,
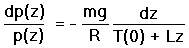 |
(9) |
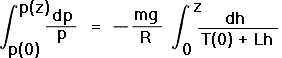 |
(10) |
In Equation (10) h is the variable of integration over altitude. The transformation of variable u = T(0) + Lh yields dh = du/L. Substitution into Equation (10) and integration yields
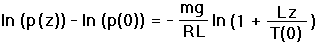 |
(11a) |
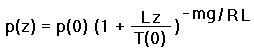 |
(11b) |
In Equation (11b) all symbols have been defined previously. Equation (11b) is the analog of Equation (7b) that accounts for a linear decline in temperature with true altitude.
Consider the effect of temperature upon pressure altitude, an effect most clearly seen upon inspection of Equations (7b,8). At lower temperature the atmosphere's scale height declines; corresponding to the observation that colder air is denser. Thus a given isosurface (surface of equal pressure) will lie at a lower true altitude in a cold environment compared to a warmer one. In a hot environment the converse occurs, and a given pressure occurs at a higher true altitude than otherwise.
This effect can be moderately large. During the Antarctic night ground temperatures are commonly -50° C (-58° F); with even lower temperatures seen every winter at interior stations. These temperatures are roughly 10-15% closer to absolute zero than are the moderate temperatures experienced elsewhere and at other times. The scale height, being reduced by some 10-15% (cf Equation (8)), results in observing the same pressure at a given elevation, as occurs at elevations 10-15% greater under moderate temperatures. Equivalently, for a given elevation, the pressure altitude will be 10-15% higher under antarctic conditions than for normal temperatures.
At the high temperature end of the climate spectrum the effect is smaller because, relative to moderate temperatures, Earth's hottest surface temperatures deviate by a smaller fraction than do Earth's lowest temperatures, all fractions calculated using the absolute zero of temperature.
Consider the effect of latitude upon pressure altitude. The acceleration due to gravity g varies with latitude from two sources described below. From Equations (7b,11b) latitude effects pressure altitude via this change in g.
Latitude effects pressure altitude indirectly from temperature changes, since clearly temperature falls in an averaged sense as one proceeds poleward. We neglect the latter, indirect effect as it is accounted for above.
The acceleration due to gravity varies with latitude from two sources. One is the centrifugal pseudo-force owing to Earth's rotation, and amounts to a 0.34% decline in g as one travels from either pole to the equator.
Earth's departure from a perfect sphere is the second source of variability. As an oblate spheroid of revolution, Earth's polar radius is less than its equatorial radius by 1 part in 298 - some 21 kilometers (13 miles). This eccentricity accounts for an additional fractional decline in g in proceeding from pole to equator. The sum, 0.53%, is a small fraction which through Equations (7-11) effects pressure altitude in a minor fashion that can be neglected for mountaineering purposes.
Over geological time Earth's rotation has caused the equatorial bulge noted above. Hence there is a feedback wherein rotation forces a minor oblateness; which in turn results in a minor shift of the gravity field.
An empirical formula is available for calculating g at any latitude
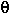 and altitude H in meters,
and altitude H in meters,
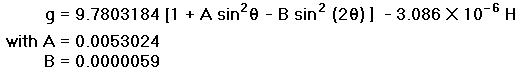 |
(12) |
The resulting values of g in meters/sec/sec are used below to compute pressure altitude deviations owing to changes in latitude.
The atmosphere's mass is negligible compared to the rocky Earth, being on the order of one-millionth the mass. Thereby Earth’s gravitational field completely dominates the local potential; and therefore determines atmospheric centripetal distortion due to rotation.
We conclude that the atmosphere's co-rotation with Earth does not meaningfully alter the effective value of g, or the pressure altitude via Equations (7b,11b). This result contrasts with statements, seen on occassion, that the atmosphere is somehow "whipped outwards" due to rotation.
In Equations (7b,7c,11b), pressure at true altitude z, as p(z), is a function of both the sea level temperature T(0) and pressure p(0). As they stand, these equations are sufficient to compute pressure altitude to any reasonable degree of accuracy, within the climbing arena, provided that the instantaneous values of T(0) and p(0) are known. To render our formulation useful, we thus require a means of specifying the statistical variations in both T(0) and p(0).
An overview of the global atmospheric circulation is provided in Appendix B. Upon reviewing that material, the reader will appreciate how very complicated our problem is were it to be addressed using a first principles approach.
In theory one could model the entire global atmosphere / ocean system and use the detailed results to provide the desired temperature and pressure variations. Such global circulation models (GCM) are used in climate forecasting and weather prediction; are extremely complicated; and require the numerical solution of the relevant three-dimensional equations on a supercomputer.
Unfortunately this approach cannot be usefully applied to modeling pressure variations at specific locations with any reasonable degree of accuracy.
We employ a far simpler, utilitarian approach that entails analysis of weather records from stations situated near major mountains. Such an approach, although not based on first principles, guarantees a more accurate portrayal of pressure variations because it is based on observation rather than a necessarily approximate theory.
Our method consists of the following steps:
These steps are now described in detail.
Temperature and Pressure Data Collection
We collect mean daily temperature and pressure recordings from the mountain of interest and/or nearby population centers. When records are only available from the latter, one demonstrates the applicability of these records to the mountain itself by near-identicality of temperature and pressure variations at two population centers located on opposite sides of the mountain.
For temperature variations, correction is made to sea level (cf Equations (7b,7c,11b)) using an environmental lapse rate of 6.5° C / km (3.57° F / 1,000 feet).
For pressure variations an altitude correction is not needed as we merely require the sea level pressure p(0) (cf Equations (7b,7c,11b)); and weather stations generally report pressures corrected to sea level anyway.
For both temperature and pressure data a least-squares fit is obtained, using day of season as the independent variable. As expected, temperature contains a large, time-dependent component, with in most cases a linear fit proving sufficient. One then demonstrates that the temperature and pressure records follow a normal distribution; and a variance about the time-dependent mean value (of temperature or pressure) is obtained.
The statistical variations in temperature and pressure are combined to obtain an overall variation (i.e. uncertainty) in the calculated pressure altitude using a modified version of Equation (11b). The derivation follows.
Denote by "A" variables pertaining to mountain A, and by "std" variables for the International Standard Atmosphere. Equation (11b) applies to both cases,
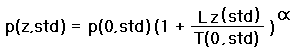 |
(11c) |
and
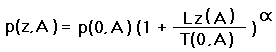 |
(11d) |
In Equations (11c,d) Greek 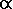 replaces the fraction -mg/RL,
and is considered a dimensionless constant for our purposes with the value 5.255753. T(std,0) is the
standard atmosphere sea level (index "0") absolute temperature (288.15° K = 518.67° R);
and T(A,0) is the sea level absolute temperature at mountain A. It is calculated
by extrapolating T(z(A)), the temperature at elevation z(A), using the environmental lapse rate:
T(A,0) = T(z(A)) + Lz(A) with L < 0.
replaces the fraction -mg/RL,
and is considered a dimensionless constant for our purposes with the value 5.255753. T(std,0) is the
standard atmosphere sea level (index "0") absolute temperature (288.15° K = 518.67° R);
and T(A,0) is the sea level absolute temperature at mountain A. It is calculated
by extrapolating T(z(A)), the temperature at elevation z(A), using the environmental lapse rate:
T(A,0) = T(z(A)) + Lz(A) with L < 0.
Setting the left sides of Equations (11c,d) equal, one solves for z(std) in terms of z(A),
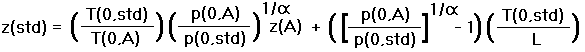 |
(13a) |
In Equation (13a) 1/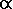 = 0.1902677 regardless
of the system of units employed.
= 0.1902677 regardless
of the system of units employed.
Trivially we obtain the difference in elevations,
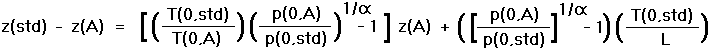 |
(13b) |
Equation (13b) is exact and is used below for the detailed tabulation of pressure altitude / true altitude differences, z(std) - z(A), at various mountains during their respective climbing seasons.
Beginning again with Equation (11b) but neglecting sea level barometric pressure variations, Equation (13a) simplifies to
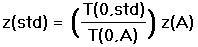 |
(13c) |
Thereby in the absence of sea level pressure differences, pressure altitude scales linearly with sea level absolute temperature.
We now approximate Equation (13b) to obtain an expression with only constants and linear functions of the arguments,
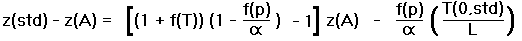 |
(14a) |
In Equation (14a) f(T) is the fractional increment in absolute temperature on proceeding from T(0,A) to T(0,std). Similarly, f(p) is the fractional increment in sea level pressure on proceeding from p(0,A) to p(0,std). The factor (1 - f(p)) approximates 1/(1 + f(p)), a valid assumption for small f(p), and arises from the 1/p(0,std) factor in Equation (13b). As these fractions never refer to any elevation other than sea level, the "0" indices in f(T) and f(p) are suppressed.
As the cross-term in f(T) x f(p) of Equation (14a) is small, we obtain the approximate expression
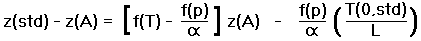 |
(14b) |
The terms in Equation (14b) are regrouped,
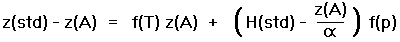 |
(14c) |
In Equation (14c) H(std) is the scale height assuming a fixed temperature T(0,std),
and replaces the factor -T(0,std)/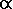 L of Equations (14a,b).
H(std) equals 8,435 meters (27,673 feet).
L of Equations (14a,b).
H(std) equals 8,435 meters (27,673 feet).
The terms in Equation (14c) have the following interpretations.
 ) f(p)
is an altitude-dependent shift in pressure altitude due to a
fractional shift in sea level pressure from A to the standard value.
These two latter shifts are equal apart from a factor of 1/
) f(p)
is an altitude-dependent shift in pressure altitude due to a
fractional shift in sea level pressure from A to the standard value.
These two latter shifts are equal apart from a factor of 1/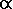 .
Hence a 1% sea level pressure shift results in only a 0.19% shift in pressure altitude
as contributed by this term.
We interpret this term as follows. With rising true altitude the temperature falls.
Hence a smaller fractional change in true altitude is required to secure a given fractional
change in pressure. At sea level only the first term in H(std) f(p) exists. The additional
term in - (z(A)/
.
Hence a 1% sea level pressure shift results in only a 0.19% shift in pressure altitude
as contributed by this term.
We interpret this term as follows. With rising true altitude the temperature falls.
Hence a smaller fractional change in true altitude is required to secure a given fractional
change in pressure. At sea level only the first term in H(std) f(p) exists. The additional
term in - (z(A)/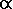 ) f(p) is the correction required to
diminish the fractional altitude change to the value appropriate for the lower temperature.
At the true altitude z(A) =
) f(p) is the correction required to
diminish the fractional altitude change to the value appropriate for the lower temperature.
At the true altitude z(A) = 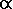 H(std) the two terms
cancel completely, having reached the height at which the absolute zero of temperature
ensures that no altitude change at all is required to secure a given fractional pressure change.
The real atmosphere's temperature rises with altitude at the tropopause - well before this
mathematical fiction takes hold at roughly 44,000 meters (145,000 feet).
H(std) the two terms
cancel completely, having reached the height at which the absolute zero of temperature
ensures that no altitude change at all is required to secure a given fractional pressure change.
The real atmosphere's temperature rises with altitude at the tropopause - well before this
mathematical fiction takes hold at roughly 44,000 meters (145,000 feet).
Using the approximate Equation (14c) rather than the exact Equation (13b), a 5% drop in extrapolated sea level temperature at mountain A relative to the Standard Atmosphere results in a 5% upshift in the Standard Atmosphere altitude, relative to A, to secure an identical pressure reading.
Similarly, a 1% drop in mean sea level pressure at mountain A relative to the Standard Atmosphere results in roughly an 84 meter (277 foot) upshift in the Standard Atmosphere altitude, relative to A, to secure an identical pressure reading. The upshift decreases linearly with true altitude at mountain A as seen above.
Variability in the sea level extrapolated temperatures and pressures at A and B are treated analogously. For example, suppose the empirically determined sea level temperature standard deviation at mountain A is ± 4° C (7 ° F). For typical values of T(0,A) this corresponds to roughly a 1.4% uncertainty in pressure altitude (cf Equation (14c)). This uncertainty increases linearly with true altitude, e.g. ± 14 meters at 1,000 meters and ± 28 meters at 2,000 meters.
Let the empirically determined sea level pressure standard deviation at mountain A be
± 8 millibars (0.23 inches Hg) - roughly a one part in 130 fractional pressure shift.
Multiplying by the scale height H(std), there results a 65 meter (213 foot)
uncertainty in pressure altitude. This value declines linearly with true altitude owing to
the term in - (z(A)/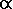 ) f(p).
) f(p).
Temperature and pressure variations from their mean values may be
correlated at a given location.
Denote by 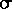 2(T)
and
2(T)
and 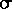 2(p)
the variance in pressure altitude from these two sources, respectively;
and computed as the squares of the temperature and pressure-derived
uncertainties in pressure altitude using Equation (14c).
Denote by
2(p)
the variance in pressure altitude from these two sources, respectively;
and computed as the squares of the temperature and pressure-derived
uncertainties in pressure altitude using Equation (14c).
Denote by 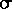 (T,p) the (possibly nonzero)
covariance of temperature and pressure.
(T,p) the (possibly nonzero)
covariance of temperature and pressure.
The total variance in pressure altitude arising from these sources is
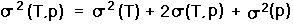 |
(15) |
If temperature and pressure variations are perfectly, positively correlated,
then 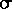 (T,p) =
(T,p) = 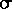 (T)
+
(T)
+ 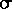 (p). For perfect negative correlation,
(p). For perfect negative correlation,
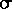 (T,p) =
(T,p) = 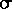 (T)
-
(T)
- 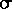 (p).
(p).
In summary, either Equations (11c,d;13a,b) or Equation (14c) is used to compute the mean shift in true altitude to encounter an identical pressure altitude in the Standard Atmosphere (or on mountain B), as found at a given true altitude on mountain A. The variance of this altitude shift is provided by Equation (15) using Equation (14c) for computing the fractional uncertainties in pressure altitude arising from both temperature and pressure variability.
The pressure altitudes corresponding to specific true altitudes at a given mountain and day are tabulated as mean values and variations about these means arising from daily temperature and pressure fluctuations. Rather than list the pressure altitudes we report differences as pressure altitude less true altitude (cf Tables 1-3).
It is also instructive to compute the true elevation on a second mountain B with the same
pressure altitude observed at the original mountain A. One uses Equation (13b)
or the approximate Equations (13c,14c), replacing the "std" indices, representing the
Standard Atmosphere, with indices "B" representing the second mountain.
H(std) in Equation (14c) is replaced by H(B) = -T(0,B)/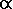 L.
L.
To find the corresponding variability in the true altitude difference z(B) - z(A), calculate the square root of the sum of the squares of the two individual variations reported in the relevant pair of tabular entries, i.e.
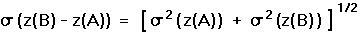 |
(16) |
In using Equation (16) we assume that observations at mountains A and B are widely separated in both time and location; such that their respective pressure and temperature variations are uncorrelated.
Mount McKinley is the most northerly of the world's big mountains. It is North America's highest summit at 6,194 meters (20,320 feet) above sea level, located in central Alaska at roughly the 63rd parallel.
We evaluate the effects of low temperature, high latitude, and variations in both temperature and sea level barometric pressure, upon pressure altitude at Mount McKinley. These pressure altitudes are compared with pressure altitudes for mountains at more southerly latitudes. For the latter we choose Aconcagua - the highest peak in South America at 6,962 meters (22,841 feet); and, representing the 7,000+ meter peaks of High Asia, Mount Everest.
The calculations are performed at two levels of detail. The first level considers just the effects of temperature and latitude. This level, although worthy of attention, is not particularly accurate as it does not include the effects of temperature and pressure variability. These calculations are included for their simplicity and ease of interpretation.
The second level of detail includes the observed statistical variations in both temperature and pressure.
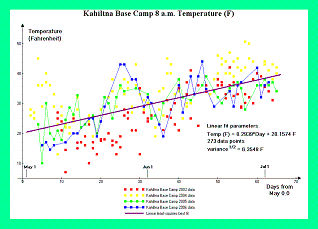
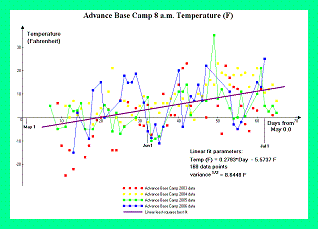
Consider the effect of temperature on pressure altitude. For Mount McKinley meteorological records from the West Buttress Route have been provided by the National Park Service.6 Figure 1 contains temperature graphs from Kahiltna Base Camp at 2,200 meters (7,200 feet) for the 2003 through 2006 climbing seasons. Figure 2 contains temperature graphs from Advance Base Camp at 4,350 meters (14,300 feet) for the same periods.
Using the environmental lapse rate of 6.5° C / km (3.57° F / 1,000 feet), one extrapolates from these observed temperatures to the theoretical, sea level temperatures which would exist at Mount McKinley's base during the climbing season - and as required in the detailed calculations.
|
|
Figure 1. Kahiltna Base Camp temperature data. (Click for a detailed view) |
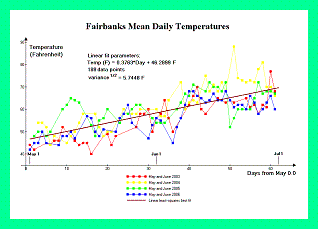
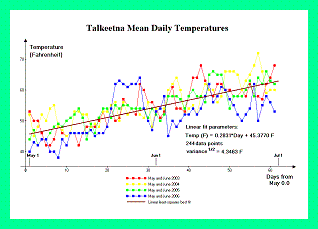
Meteorological data from nearby population centers corroborate the estimated sea level temperatures. For Mount McKinley, data is available for both Fairbanks and Talkeetna, Alaska - two communities on opposite sides of the Alaska Range. Figure 3 contains temperature graphs from Fairbanks, Alaska (elevation 138 meters = 453 feet) for May and June of 2003 through 2006; and corresponding to the climbing season at Mount McKinley. Figure 4 contains temperature graphs for Talkeetna, Alaska (elevation 109 meters = 358 feet) with the same time periods.
|
|
Figure 2. Advance Base Camp temperature data. (Click for a detailed view) |
We obtain 10.3° C (50.5° F) and 15.6° C (60° F) for Mount McKinley's theoretical sea level temperature in May and June, respectively; and 27° C (80° F) for the comparison mountains. Note the 5.3° C (9.5° F) change in one month for Mount McKinley. Values are based on the mean daily temperatures at May 15 and June 15, using the linear least-squares best fits for the eight months of available data (May and June for 2003 through 2006). Daily maxima and minima are typically 5.5° C (10° F) higher and lower than these mean values, respectively.
These mean, extrapolated sea level temperatures are substituted into Equation (13c). The fractional drop in absolute temperature at sea level between the comparison mountains and Mount McKinley yields a 5.8% and 3.8% higher pressure altitude at Mount McKinley, for a given true altitude, compared with the more southerly peaks, for May 15 and June 15, respectively.
|
|
Figure 3. Fairbanks temperature data. (Click for a detailed view) |
At the 6,194 meter (20,320 foot) summit these fractions correspond to 360 meters (1,175 feet) and 240 meters (780 feet) of additional pressure altitude relative to the same true altitude on the comparison mountains, all peaks being considered during their respective optimal climbing seasons.
At the 5,250 meter (17,200 foot) high camp on the West Buttress Route these fractions correspond to 305 meters (995 feet) and 200 meters (660 feet) of additional pressure altitude relative to the same true altitude on the comparison mountains.
These true altitude differences between locations at identical pressure altitudes are approximate in that variability in temperature and sea level barometric pressure have not been accounted for. This variability is considered in the next section.
|
|
Figure 4. Talkeetna temperature data. (Click for a detailed view) |
Consider the effect of latitude on pressure altitude. The Himalaya and Karakoram Ranges closely straddle 30° N; and Aconcagua lies near 33° S - roughly the latitude of San Diego, California apart from sign. We use 30 degrees north or south as representative of these mountains.
Substitution of  = 30° and
= 30° and
 = 63° into Equation (12) yields a fractional shift of
0.0029 in the resulting values of g. The acceleration due to gravity at Mount McKinley
is 0.29% more than at 30° north or south.
= 63° into Equation (12) yields a fractional shift of
0.0029 in the resulting values of g. The acceleration due to gravity at Mount McKinley
is 0.29% more than at 30° north or south.
From Equation (7b) a given pressure altitude will exist at Mount McKinley at an elevation 0.29% lower compared with the more southerly mountains due to the effect of latitude.7 Equivalently, at a given true altitude, the pressure altitude at Mount McKinley will be 0.29% higher compared with the more southerly mountains - again due to latitude alone.
Most climbers ascend Mount McKinley via the West Buttress Route. The highest camp normally established is located at 5,250 meters (17,200 feet). Multiplying this elevation by 0.29%, latitude alone, and hence the combined effects of centrifugal force and other sources for variation in g, results in a negligible 15 meters (50 feet) additional pressure altitude compared with the same elevation on both Aconcagua and peaks in High Asia. This result is true for all seasons. At Mount Mckinley's summit the additional pressure altitude is 18 meters (60 feet).
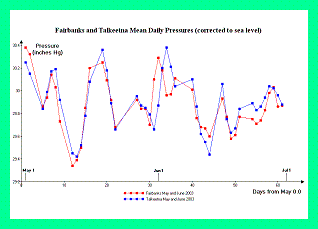
Temperature and pressure variations contribute to the observed pressure altitude at Mount McKinley and other mountains. Whereas temperature data is available for the West Buttress climbing route, pressure must be estimated based upon meteorological records from the nearby population centers of Fairbanks and Talkeetna, Alaska.
Linear least-squares analyses show no trend with day of season for the mean, sea level-corrected pressures at these communities. Mean daily pressure equals that of the Standard Atmosphere to within the current work's desired accuracy - roughly 15 or 30 meters in altitude (50 or 100 feet).
|
|
Figure 5. Fairbanks and Talkeetna 2003 pressure data. (Click for a detailed view) |
An essential component of this analysis is the assumption that sea level pressure variations at Mount McKinley are similar to those at nearby population centers for which pressure data is available. Without some estimate of both sea level-corrected pressure, and of its variability, no further analysis is possible.
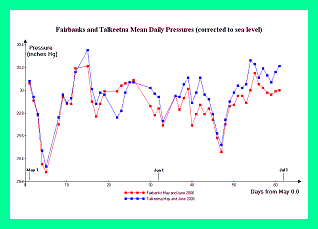
Figure 5 contains graphs of mean daily pressure, corrected to sea level, at both Fairbanks and Talkeetna, for May and June 2003. Figure 6 contains analogous graphs for the calendar 2006 climbing season. In both graphs the daily and weekly high and low pressure variations are nearly identical upon comparing the two communities. As Mount McKinley lies in-between these two communities, the sea level-corrected pressure there must be nearly identical.
For the detailed calculations we use for Mount McKinley the mean of the Fairbanks and Talkeetna standard deviations in pressure as pooled over the May and June months of 2003-2006. The Fairbanks and Talkeetna pressure standard deviations over these eight months are 7.59 and 7.79 millibars (0.2241 and 0.2301 inches Hg) respectively.
|
|
Figure 6. Fairbanks and Talkeetna 2006 pressure data. (Click for a detailed view) |
As the mean sea level-corrected pressure at both Fairbanks and Talkneetna equals that for the Standard Atmosphere, Equation (13c) is used to compute the mean pressure altitude at various West Buttress camps on Mount McKinley, and for the summit. The more elaborate Equation (13b) would be used had a significant difference existed between the measured mean sea level-corrected pressure and the Standard Atmosphere.
Standard deviations in both mean daily temperature and mean daily pressure are used to compute the overall deviations in pressure altitudes at various camps on Mount McKinley, and for the summit, using Equations (14c,15,16).
Table 1 presents both the pressure altitudes and their standard deviations for these camps and the summit, expressed as pressure altitude minus true altitude differences. The calculations are performed using mean temperatures on five calendar days spanning the May and June climbing season.
Table 1. Mount McKinley pressure altitude / true altitude differences in meters (feet). Variabilities (after the "±" signs) correspond to one standard deviation.a
| May 1 | May 15 | June 1 | June 15 | July 1 | |
| Kahiltna Base Camp 2,200 meters (7,200 feet) |
55 ± 64 (182 ± 211) |
37 ± 64 (120 ± 211) |
14 ± 64 ( 46 ± 210) |
-4 ± 64 (-14 ± 210) |
-25 ± 64 (-81 ± 210) |
| Advance Base Camp 4,350 meters (14,300 feet) |
110 ± 90 ( 362 ± 294) |
73 ± 89 ( 238 ± 293) |
28 ± 89 ( 91 ± 291) |
-8 ± 88 ( -28 ± 289) |
-49 ± 88 (-161 ± 288) |
| West Buttress High Camp 5,250 meters (17,200 feet) |
133 ± 111 ( 435 ± 365) |
87 ± 110 ( 287 ± 362) |
33 ± 110 ( 110 ± 360) |
-10 ± 109 ( -33 ± 357) |
-59 ± 108 (-194 ± 355) |
| Summit 6,194 meters (20,320 feet) |
157 ± 140 ( 514 ± 458) |
103 ± 139 ( 339 ± 455) |
40 ± 137 ( 130 ± 451) |
-12 ± 136 ( -39 ± 448) |
-70 ± 135 (-229 ± 444) |
aTo account for latitude via a shift in g, add these constants to the entries in Table 1: Kahiltna Base Camp 3 meters (11 feet); Advance Base Camp 7 meters (22 feet); West Buttress high camp 8 meters (26 feet); summit 9 meters (31 feet).
|
|
Figure 7. Mendoza, Argentina temperature data. (Click for a detailed view) |
Analogous prescriptions for computing pressure altitude are applied to other mountains and mountain ranges as described here.
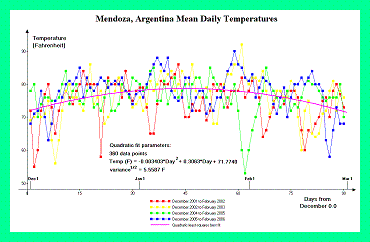
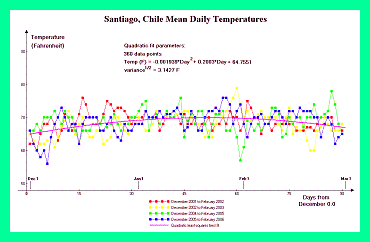
Mendoza, Argentina and Santiago, Chile are two cities that lie on opposite sides of the Andean Cordillera. Hence they comprise an appropriate set for estimating pressure at Aconcagua just as do Fairbanks and Talkeetna, Alaska for Mount McKinley. Figure 7 contains temperature graphs from Mendoza, Argentina (elevation 704 meters = 2,310 feet) for December through February of four austral summers, corresponding to the Aconcagua climbing season. Figure 8 contains temperature graphs for Santiago, Chile (elevation 476 meters = 1,562 feet) for the same periods.
As the Aconcagua climbing season straddles the southern Hemisphere's summer solstice, a maximum in temperature is observed mid-season with a slightly lower mean temperature to either side - an inverted parabola. Hence both Mendoza and Santiago temperature data are better fit with a quadratic curve.
|
|
Figure 8. Santiago, Chile temperature data. (Click for a detailed view) |
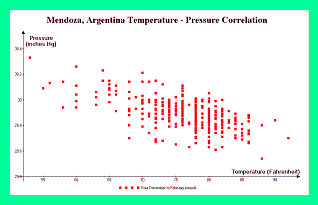
The Mendoza data exhibits an unusually large, negative pressure-temperature cross-correlation (-0.6430). The cross-correlation is computed using observed deviations from the quadratic least-squares best fits to both pressure and temperature, i.e. it is not computed using deviations from the mean pressure and mean temperature as averaged over the entire season. Nevertheless, as seen in Figure 9 a simple graph of pressure versus temperature shows how striking this correlation is, even though the graph's production did not account for the seasonal-dependence of mean pressure and temperature.
|
|
Figure 9. Mendoza, Argentina pressure-temperature cross-correlation. (Click for a detailed view) |
The Santiago data exhibits unusually small departures in both pressure and temperature (cf Figure 8). The coastal location, with consequent moderating influence of the ocean on climate, explains this result.
Table 2 presents both the pressure altitudes and their standard deviations for various Aconcagua camps and the summit, expressed as pressure altitude minus true altitude differences. The calculations are performed using mean temperatures on five calendar days covering the December through February climbing season, and are based on the Mendoza, Argentina and Santiago, Chile datasets.
Table 2. Aconcagua pressure altitude / true altitude differences in meters (feet). Variabilities (after the "±" signs) correspond to one standard deviation.a
| December 15 | January 1 | January 15 | February 1 | February 15 | |
| Puente del Inca roadhead 2,750 meters (9,000 feet) |
-98 ± 22 (-322 ± 72) |
-107 ± 22 (-351 ± 72) |
-108 ± 22 (-354 ± 72) |
-102 ± 22 (-334 ± 72) |
-91 ± 22 (-298 ± 72) |
| Ruta Normal Base Camp 4,350 meters (14,300 feet) |
-156 ± 31 (-513 ± 101) |
-171 ± 31 (-562 ± 100) |
-174 ± 31 (-572 ± 100) |
-166 ± 31 (-545 ± 100) |
-150 ± 31 (-493 ± 100) |
| Nido de Condores 5,500 meters (18,000 feet) |
-197 ± 38 (-647 ± 126) |
-216 ± 38 (-710 ± 125) |
-221 ± 38 (-723 ± 125) |
-211 ± 38 (-693 ± 125) |
-192 ± 38 (-629 ± 126) |
| Camp Berlin 5,950 meters (19,450 feet) |
-213 ± 42 (-699 ± 136) |
-234 ± 41 (-768 ± 136) |
-239 ± 41 (-783 ± 136) |
-229 ± 41 (-750 ± 136) |
-208 ± 42 (-682 ± 136) |
| Summit 6,962 meters (22,841 feet) |
-250 ± 49 (-821 ± 162) |
-275 ± 49 (-903 ± 161) |
-281 ± 49 (-922 ± 161) |
-270 ± 49 (-885 ± 161) |
-246 ± 49 (-806 ± 162) |
aTo account for latitude via a shift in g, add these constants to the entries in Table 2: Puente del Inca -3 meters (-10 feet); Ruta Normal Base Camp -5 meters (-16 feet); Nido de Condores -6 meters (-21 feet); Camp Berlin -7 meters (-22 feet); summit -8 meters (-26 feet).
Kathmandu, Nepal meteorological data is used for estimating pressure altitudes at Mount Everest - the mountain chosen as representative of High Asia. It was desired to balance these records with analogous data from Tibet. Unfortunately daily meteorological observations are not readily available for this region.
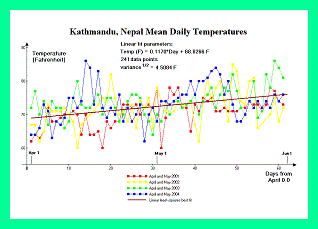
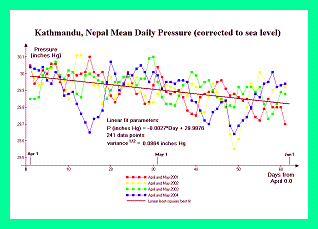
Figure 10 contains temperature graphs from Kathmandu, Nepal (elevation 1,337 meters = 4,386 feet) for April and May of four consecutive Mount Everest climbing seasons. Figure 11 contains pressure graphs for Kathmandu over the same periods.
|
|
Figure 10. Kathmandu, Nepal temperature data. (Click for a detailed view) |
The Kathmandu data exhibits a marked decrease in sea level pressure as the season progresses (cf Figure 11); and corresponds to the approaching monsoon season. The temperature data exhibits an increase in mean value as the summer solstice is approached (cf Figure 10).
The temperature and pressure are negatively correlated with a cross-correlation of -0.3467 as summed over the four seasons examined. This negative correlation does not correspond to the obvious, secular trend of diminishing pressures and rising temperatures as the seasons progress. Rather, individual deviations of pressure and temperature from their respective moving averages are negatively correlated.
|
|
Figure 11. Kathmandu, Nepal pressure data. (Click for a detailed view) |
Table 3 presents both the pressure altitudes and their standard deviations for various Mount Everest camps and the summit, expressed as pressure altitude minus true altitude differences. The calculations are performed using mean temperatures on five calendar days spanning the April and May climbing season, and are based on the Kathmandu, Nepal data.
In Table 1 baseline pressure altitudes, i.e. without considering their variabilities, are both higher and lower than the true altitudes for Mount McKinley. However in Tables 2 and 3 baseline pressure altitudes are always lower for both Aconcagua and High Asia (the latter represented by Mount Everest). This point is discussed at length in the next section.
There are 20 entries in Table 1 for the Mount McKinley pressure altitude, as the product of four elevations and five days spaced over the climbing season. Similarly, there are 25 entries in Table 2 for Aconcagua; and 25 in Table 3 for High Asia.
Table 3. High Asia pressure altitude / true altitude differences in meters (feet) as represented by Mount Everest. Variabilities (after the "±" signs) correspond to one standard deviation.a
| April 1 | April 15 | May 1 | May 15 | June 1 | |
| Lukla, Nepal 2,850 meters (9,380 feet) |
-116 ± 27 (-380 ± 87) |
-135 ± 27 (-444 ± 87) |
-157 ± 26 (-516 ± 87) |
-177 ± 26 (-580 ± 87) |
-200 ± 26 (-656 ± 87) |
| Base Camp (Nepalese side) 5,350 meters (17,600 feet) |
-233 ± 42 ( -765 ± 138) |
-260 ± 42 ( -854 ± 138) |
-291 ± 42 ( -956 ± 137) |
-318 ± 42 (-1044 ± 137) |
-351 ± 42 (-1151 ± 136) |
Advance Base Camp (Tibetan side) 6,500 meters (21,300 feet) |
-286 ± 50 ( -939 ± 166) |
-317 ± 50 (-1039 ± 165) |
-352 ± 50 (-1154 ± 165) |
-382 ± 50 (-1253 ± 164) |
-419 ± 50 (-1374 ± 163) |
| South Col 7,925 meters (26,000 feet) |
-353 ± 62 (-1159 ± 202) |
-388 ± 61 (-1274 ± 202) |
-428 ± 61 (-1405 ± 201) |
-463 ± 61 (-1519 ± 200) |
-505 ± 61 (-1657 ± 200) |
| Summit 8,848 meters (29,028 feet) |
-397 ± 69 (-1301 ± 226) |
-434 ± 69 (-1425 ± 226) |
-478 ± 69 (-1567 ± 225) |
-515 ± 68 (-1690 ± 224) |
-560 ± 68 (-1839 ± 223) |
aTo account for latitude via a shift in g, add these constants to the entries in Table 2: Lukla -4 meters (-14 feet); Base Camp (Nepal) -8 meters (-27 feet); Advance Base Camp (Tibet) -10 meters (-32 feet); South Col -12 meters (-40 feet); summit -13 meters (-44 feet).
Direct tabulation of true elevation differences required for observing the same pressure on pairs of mountains would entail a table with as many entries as the pairwise products of the numbers of entries in Tables 1 through 3. For example, High Camp on Mount McKinley on May 15 and Camp Berlin on Aconcagua on January 31 would be one of 20 x 25 = 500 entries in a Mount McKinley - Aconcagua comparison chart. A different table would be required for each pairwise mountain combination, i.e. Mount McKinley - High Asia and Aconcagua - High Asia.
By presenting the results in terms of pressure altitudes in the Standard Atmosphere, one mountain at a time, this needless proliferation of print is avoided. One must, however, apply the prescription of the Section "Tabulation of Calculated Altitude Differences".
Nevertheless it is instructive to directly compare the true altitudes on pairs of mountains for which the pressure altitudes are identical. This exercise is of inherent interest to high altitude climbers and expeditions. We render it practical within this article by limiting consideration to one true altitude: the summit of Mount McKinley. In so doing the combinatorial explosion described above is obviated.
In Table 4 differences in true altitudes required to match Mount McKinley's summit pressure altitude are presented for Aconcagua as the comparison mountain. To compute these differences the prescription of the Section "Tabulation of Calculated Altitude Differences" is employed.
Table 4. Mount McKinley / Aconcagua true altitude differences in meters (feet) for matching pressures at the summit of Mount McKinley. Rows are calendar days during the Mount McKinley climbing season; and columns similarly for Aconcagua. Variabilities (after the "±" signs) correspond to one standard deviation.a
| December 15 | January 1 | January 15 | February 1 | February 15 | |
| May 1 | 393 ± 147 (1291 ± 483) |
418 ± 147 (1371 ± 483) |
423 ± 147 (1389 ± 483) |
412 ± 147 (1353 ± 483) |
388 ± 147 (1274 ± 483) |
| May 15 | 338 ± 146 (1109 ± 479) |
362 ± 146 (1189 ± 479) |
368 ± 146 (1207 ± 479) |
357 ± 146 (1170 ± 479) |
333 ± 146 (1093 ± 479) |
| June 1 | 272 ± 145 (892 ± 475) |
296 ± 145 (971 ± 475) |
301 ± 145 (989 ± 475) |
290 ± 145 (953 ± 475) |
267 ± 145 (876 ± 475) |
| June 15 | 219 ± 144 (717 ± 472) |
242 ± 144 (795 ± 472) |
248 ± 144 (813 ± 472) |
237 ± 144 (777 ± 472) |
214 ± 144 (700 ± 471) |
| July 1 | 159 ± 143 (521 ± 468) |
182 ± 143 (598 ± 468) |
187 ± 143 (615 ± 468) |
177 ± 143 (579 ± 468) |
154 ± 143 (504 ± 468) |
aTo account for latitude via a shift in g, add 17 meters (55 feet) to all tabulated values.
In Table 5 differences in true altitudes required to match Mount McKinley's summit pressure altitude are presented for High Asia, using Mount Everest as the comparison mountain.
Table 5. Mount McKinley / High Asia true altitude differences in meters (feet) for matching pressures at the summit of Mount McKinley. Rows are calendar days during the Mount McKinley climbing season; and columns similarly for High Asia. Variabilities (after the "±" signs) correspond to one standard deviation.a
| April 1 | April 15 | May 1 | May 15 | June 1 | |
| May 1 | 450 ± 149 (1476 ± 489) |
483 ± 149 (1583 ± 489) |
520 ± 149 (1706 ± 489) |
553 ± 149 (1814 ± 489) |
593 ± 149 (1946 ± 489) |
| May 15 | 394 ± 148 (1292 ± 485) |
426 ± 148 (1399 ± 485) |
464 ± 148 (1521 ± 485) |
496 ± 148 (1628 ± 486) |
536 ± 148 (1759 ± 486) |
| June 1 | 327 ± 147 (1073 ± 481) |
359 ± 147 (1179 ± 481) |
396 ± 147 (1301 ± 481) |
429 ± 147 (1407 ± 481) |
468 ± 147 (1537 ± 481) |
| June 15 | 273 ± 145 ( 896 ± 477) |
305 ± 146 (1001 ± 477) |
342 ± 146 (1122 ± 478) |
374 ± 146 (1228 ± 478) |
414 ± 146 (1357 ± 478) |
| July 1 | 212 ± 144 ( 697 ± 473) |
244 ± 144 ( 802 ± 473) |
281 ± 144 ( 922 ± 474) |
313 ± 144 (1027 ± 474) |
352 ± 144 (1156 ± 474) |
aTo account for latitude via a shift in g, add 19 meters (63 feet) to all tabulated values.
The entries in Tables 4 and 5 are not simply the difference of the corresponding, relevant entries in Tables 1 through 3. Specifically, Tables 2 and 3 pertain to specific true altitudes on the comparison mountains, corresponding to established camps - and these camps are not located at the exact pressure altitudes for Mount McKinley's summit.
The magnitudes and seasonal trends in true altitude differences of Tables 4 and 5 are important results discussed below.
The current work uses a first principles approach to calculate pressure altitude. The resulting variables include both sea-level temperature and pressure; and the acceleration due to gravity.
This approach has the advantage of not introducing error arising from applying a geophysical model developed for a specific latitude/season combination; and applying it to a montane setting at a slightly different latitude and time of year.
For example, models exist for specifying the temperature/pressure profiles of the atmosphere at 30° N during January and July.1 However neither of these months correspond to the Himalaya climbing season. As Mount Everest is normally scaled in May and October, the use of a July profile to represent conditions in May introduces error - albeit likely a slight one.
The current work prescribes a method for calculating pressure altitude without being straightjacketed into finding that geophysical model which most closely approximates the time and location of interest.
Our work suffers from the need to secure meteorological observations near and/or at the mountain of interest.
Pressure altitude is computed for various true altitudes on Mount McKinley, with analogous results obtained at Aconcagua and High Asia for comparison. The calculations are performed at two levels of theory - without and with account of variability in temperature and sea level-corrected barometric pressure.
During the May and June climbing season, Mount McKinley's summit pressure altitude declines from a mean value of 157 meters (514 feet) higher than the true altitude, to 70 meters (229 feet) lower than the true altitude (Table 1). This seasonal trend results from rising sea level temperatures as extrapolated from the detailed meteorological data (Figures 1-4). Daily temperature variations modify these values with a standard deviation of roughly 140 meters (450 feet). These pressure altitude / true altitude differences are not particularly large compared with the true altitude of 6,194 meters (20,320 feet).
The summit pressure altitude atop Mount McKinley is on average 115 meters (378 feet) lower June 15 compared to May 15. The average summit pressure altitude is 227 meters (743 feet) lower July 1 compared to May 1. Swings in pressure altitude owing to regional weather patterns (mainly via temperature shifts) will cause variability about these mean values.
These observations should be noted by all those contemplating an ascent of Mount McKinley.
During the December through February climbing season, Aconcagua's summit pressure altitude declines from a mean value of 250 meters (821 feet) lower than the true altitude; to a mean value mid-season of 289 meters (922 feet) lower than the true altitude; and then rises to a mean value of 246 meters (806 feet) lower than the true altitude (Table 2). This trend results from rising and then diminishing sea level temperatures as extrapolated from the detailed meteorological data (Figures 7,8). Daily temperature variations modify these values with a standard deviation of roughly 50 meters (160 feet). These pressure altitude / true altitude differences are not particularly large compared with the true altitude of 6,962 meters (22,841 feet) - but are larger in magnitude than the corresponding differences at Mount McKinley.
During the April and May climbing season, Mount Everest's summit pressure altitude declines from a mean value of 397 meters (1,301 feet) lower than the true altitude; to 560 meters (1,839 feet) lower than the true altitude (Table 3). This seasonal trend results from rising sea level temperatures, and declining sea level-corrected pressures (Figures 10,11). Daily temperature variations modify these values with a standard deviation of roughly 70 meters (225 feet). These pressure altitude / true altitude differences, although not particularly large compared with the true altitude of 8,848 meters (29,028 feet), are larger in magnitude than the corresponding differences at Mount McKinley and Aconcagua.
It is extremely noteworthy that all pressure altitudes at Aconcagua and Mount Everest, during their respective climbing seasons, are lower than the true altitude (Tables 2,3). In contrast, pressure altitudes at Mount McKinley are at first slightly higher than the true altitude; and then, at season's end, slightly lower than the true altitude (Table 1).
Most mountains are climbed during the warmer months of their respective hemispheres. Hence is it anticipated, and observed, that pressure altitudes will tend to be lower than true altitudes because during these months temperatures are higher than the Standard Atmosphere. The higher temperatures raise the scale height (cf Equations (7c,8)) and hence diminish the perceived pressure altitude.
Mount McKinley, lying so far north, forms an exception in that even during its optimal season temperatures are tolerably similar to the Standard Atmosphere. Thus pressure altitudes are either marginally higher (May) or lower (late June) than the corresponding true altitudes.
Dr. West was aware of the role warmer months play in skewing the availability of pressure data from montane settings.3 He was also aware that the Standard Atmosphere tends to understimate the calculated pressure atop high mountains; in turn because they are generally climbed in their respective warmer months when the temperature exceeds that predicted by the Standard Atmosphere.
In Table 4 direct comparison is made of true elevations at which the same pressure altitudes are observable on Mount McKinley and Aconcagua. The central entry of that table represents the middle of their respective climbing seasons. Using that entry, one must be an average of 301 meters (989 feet) higher on Aconcagua to observe the same pressure as at the summit of Mount McKinley - 6,495 meters (21,309 feet). Earlier days in the Mount McKinley climbing season, such as May 1, result in larger true altitude differences approaching 400 meters (1,300 feet).
In Table 5 direct comparison is made of true elevations at which the same pressure altitudes are observable on Mount McKinley and, representing High Asia, Mount Everest. The central entry of that table represents the middle of their respective climbing seasons. Using that entry, one must be an average of 396 meters (1,301 feet) higher on Mount Everest to observe the same pressure as at the summit of Mount McKinley - 6,590 meters (21,621 feet). Earlier days in the Mount McKinley climbing season, such as May 1; and/or later days in the Mount Everest climbing season, result in larger true altitude differences approaching 600 meters (1,950 feet).
For both Aconcagua and High Asia, variabilities of these true altitude differences are roughly ± 145 meters (475 feet) at one standard deviation (Tables 4,5).
Noting this variability, from the bottom row of Table 4 it is possible in late June for the pressure altitude at Mount McKinley's summit to be observed on Aconcagua's slopes in December and February at the same 6,194 meter elevation (20,320 feet).
Noting this variability, from the top row of Table 5 it is possible in early May for the pressure altitude at Mount McKinley's summit to be observed at 6,900 meters (22,600 feet) on Mount Everest's slopes in May - 700 meters (2,300 feet) higher than Mount McKinley's summit elevation.
These true altitude differences for matching summit pressure are not due to colder than standard temperatures at Mount McKinley. The differences arise from warmer than standard temperatures at the comparison mountains.
Recall that Dr. Moore considered the effect of low temperature upon barometric pressure for Earth's highest mountains in a 1968 paper.2 Comparing Mount McKinley summit pressure with the Himalaya, he reported pressure altitudes similar to those calculated here. In the summer Mount McKinley's summit pressure was estimated equivalent to being 400 meters (1,300 feet) higher in the summer Himalaya - 6,600 meters (21,650 feet). This pressure altitude is equivalent to that obtained in Table 5 as the central entry.
In the winter Mount McKinley's summit pressure was estimated equivalent to being a full 950 meters (3,100 feet) higher in the summer Himalaya - 7,150 meters (23,450 feet). This latter value is obtained in the present formulation by using a sea level temperature T(0) = -13° C (8° F) for interior Alaska by winter, and 27° C (80° F) for the comparison Asian mountains.8
Although it is possible than in his pioneering paper Dr. Moore used a formulation similar to the current one based on Equations (7c,11b), there is nothing readily evident in the manuscript to suggest this.2 The values of pressure altitude as a function of latitude appear to be interpolated from tabulated data.
If Dr. Moore's article was limited by interpolation of known data, then the present work both provides a theoretical basis for his, and corroborates it through independent calculation.
This temperature-dependence of pressure arises anywhere and anytime - not just on Mount McKinley. Ascending a 14,000 foot mountain in Colorado by winter will meet with a lower atmospheric pressure enroute and at the summit compared with a summer hike. The effect's magnitude is given by the fractional decrease in extrapolated sea level temperature relative to summer.
An extreme example of temperature influencing pressure altitude is given by winter on the Antarctic plateau. Vostok Station has recorded the coldest surface temperatures on Earth. At 3,420 meters (11,220 feet), Vostok has ample elevation and sufficiently low temperatures to support a large pressure altitude / true altitude difference (cf Equation (13c)). From roughly April through September the mean daily temperature is typically -65° C (-85° F). Substitution into Equation (13c) yields a pressure altitude of 4,280 meters (14,035 feet) - fully 860 meters (2,815 feet) higher than the true altitude!
Deviations in mean, sea-level corrected pressures between the various mountains of this article are extremely minor - some three powers of ten less than the pressure itself. These deviations have negligible effects on calculated pressure altitude differences.
Latitude, via a shift in the acceleration due to gravity, causes a change in pressure altitude from a combination of centrifugal force and mass-distribution effects arising from Earth's eccentricity.
Account of latitude raises the pressure altitude at Mount McKinley's summit 17 meters (55 feet) relative to Aconcagua (cf footnote Table 4). Account of latitude raises the pressure altitude at Mount McKinley's summit 19 meters (63 feet) relative to Mount Everest (cf footnote Table 5). These changes in pressure altitude are minor, and have little consequence for those climbing the world's higher mountains.
In the climbing literature on Mount McKinley (and apart from Dr. Moore's work), the claim is made that breathing is more arduous for a given altitude because centrifugal force due to Earth's rotation is less than for more temperately located mountains. The atmosphere is "whipped outwards" at the equator, raising the scale height with a resulting higher pressure for a given true altitude.
A centrifugal effect indeed manifests itself by a change in the effective value of g, with g diminished slightly at the equator where the speed of rotation is greatest. From Equation (12) g rises only 0.53% between equator and either pole; with 0.34% of this increase due to diminished centrifugal force with latitude. From Equations (7b,8) all pressure altitudes shift this small fraction as a result of Earth's rotation - roughly one part in 300.
For the summits of two 6,000 meter (19,700 foot) mountains, one at the equator and one at either pole, this fraction corresponds to a 20 meter (66 foot) pressure altitude difference. The pressure altitude correction is normally even smaller still since most mountains are not located exactly on the equator or in the polar regions.
Thus the claim that Earth's rotation is the cause of lower air pressure near the poles is false. Lower air temperature is the overwhelmingly important cause.
At extreme altitudes even a slight shift in pressure altitude elicits a large shift
in physiological performance.9 Hence a prudent choice of atmospheric model
is critical. The key variables are inspired oxygen partial pressure
PI,O2, and the rate of maximal oxygen consumption per kilogram
 O2 max.
O2 max.
The equations relating these variables are derived in
Appendix C. Equation (C.3d) is the key result, expressing the
total derivative of  O2 max
with respect to the atmospheric scale height H using the simplified expressions
of Equations (7c,8). The more accurate Equation (11b) is not used because measured
O2 max
with respect to the atmospheric scale height H using the simplified expressions
of Equations (7c,8). The more accurate Equation (11b) is not used because measured
 O2 max values
are of insufficient detail to warrant such an accurate description.
O2 max values
are of insufficient detail to warrant such an accurate description.
The derivative of Equation (C.3d) is the sum of two terms. One is the explicit derivative of
 O2 max
with respect to PI,O2,
and is given by the first term on the right hand side thereof.
The second term, a sum, is the implicit derivative of
O2 max
with respect to PI,O2,
and is given by the first term on the right hand side thereof.
The second term, a sum, is the implicit derivative of
 O2 max
with respect to PI,O2 changes via the accompanying
nonlinear shifts in physiological variables. PI,O2
is effectively a surrogate for pressure altitude, there being a simple exponential relation
between the two (cf Appendix C footnote [1]).
O2 max
with respect to PI,O2 changes via the accompanying
nonlinear shifts in physiological variables. PI,O2
is effectively a surrogate for pressure altitude, there being a simple exponential relation
between the two (cf Appendix C footnote [1]).
Equation (C.3d) is completely general, making no assumptions about the complicated internal physiological mechanisms at-play upon sojourning to high altitudes.
In a landmark research effort, several fit volunteers were subjected to a simulated 40 day "ascent" of Mount Everest in a decompression chamber.10 Maximum exercise performance was measured at various pressure altitudes.
Equation (C.3d) is applied to that data, the required total derivatives of
 O2 max
with respect to PI,O2 being simply the differences of
O2 max
with respect to PI,O2 being simply the differences of
 O2 max
at adjacent data points, divided by the corresponding differences in
PI,O2.
O2 max
at adjacent data points, divided by the corresponding differences in
PI,O2.
In that study, the lowest PI,O2 values were 49 and 43 Torr; and correspond to altitudes in the ICAO model atmosphere of 7,622 meters (25,000 feet) and 8,382 meters (27,500 feet) respectively. The 43 Torr pressure was intentionally selected to correspond to the 253 Torr barometric pressure observed at the summit of Mount Everest - a value considerably higher than predicted using the ICAO model.
For these two data points one obtains from Equation (C.3d) a fractional shift in
 O2 max
of 4.98 x 10-4 for every meter shift in the atmospheric scale height H.11,12
O2 max
of 4.98 x 10-4 for every meter shift in the atmospheric scale height H.11,12
Using the simple prescription of Equations (7c,8), the observed summit pressure of 253 Torr
corresponds to an atmospheric scale height of 8,036 meters (26,365 feet).11
In contrast, the scale height of the ICAO standard atmosphere is 7,685 meters (25,213 feet).
Multiplying by 4.98 x 10-4 / meter, the 351 meter difference yields a substantial
17.5% decrement in  O2 max
were Mount Everest to be scaled under ICAO standard conditions.
O2 max
were Mount Everest to be scaled under ICAO standard conditions.
As it is obtained by a numerical first-difference, this 17.5% decline corresponds to climbing at a
simulated altitude midway between the 49 and 43 Torr data points -
8,391 meters (27,530 feet) under the test conditions applied. As the slope of the
 O2 max vs
PI,O2 curve steepens with altitude,
a slightly larger fractional decline is expected at the summit.
O2 max vs
PI,O2 curve steepens with altitude,
a slightly larger fractional decline is expected at the summit.
From Equation (8) the absolute temperature T and scale height H are related by the constant
factor R / mg = 29.272 meters / °K. Multiplying the right hand side of Equation (C.3d)
by this factor, one obtains the fractional shift in
 O2 max
for every degree centigrade shift in the ambient temperature.
O2 max
for every degree centigrade shift in the ambient temperature.
In the current example this yields a 1.46% / °C fractional shift in
 O2 max.
This value is substantial, pointing out yet another obstacle to high altitude winter ascents;
while underscoring the importance of using the correct atmospheric model for
high altitude physiology studies.
O2 max.
This value is substantial, pointing out yet another obstacle to high altitude winter ascents;
while underscoring the importance of using the correct atmospheric model for
high altitude physiology studies.
Dr. West reached similar conclusions for the decrement in
 O2 max
under ICAO standard conditions, using data from the 1981
American Medical Research Expedition to Everest II (AMREE),13,14 and from a
1997 NOVA expedition.15
The following excerpt from [15] is highly relevant, reproduced here with author permission.
O2 max
under ICAO standard conditions, using data from the 1981
American Medical Research Expedition to Everest II (AMREE),13,14 and from a
1997 NOVA expedition.15
The following excerpt from [15] is highly relevant, reproduced here with author permission.
"The extreme steepness of the line relating O2 max to inspired PO2 has some interesting physiological implications. For example, if the barometric pressure on the summit were 236 Torr, as predicted from the International Civil Aviation Organization Standard Atmosphere (2), the inspired PO2 on the summit would be only 39.5 Torr. Therefore, the reduction in inspired PO2 from the value of 43 Torr, which would exist for a summit pressure of 253 Torr, would be 3.5 Torr. The reduction of oxygen consumption would therefore be about 222 ml/min to a value of about 848 ml/min, or a reduction of about 21%. It seems very unlikely that the mountain could be climbed under these conditions."
The slope of the  O2 max
vs PI,O2 curve increases with altitude.
A graph of the fractional change in
O2 max
vs PI,O2 curve increases with altitude.
A graph of the fractional change in
 O2 max
vs PI,O2 is expected to have an even larger magnitude slope
for extreme altitudes, having divided by the additional factor
O2 max
vs PI,O2 is expected to have an even larger magnitude slope
for extreme altitudes, having divided by the additional factor
 O2 max
which diminishes with altitude.
O2 max
which diminishes with altitude.
Thereby it is fitting that at Mount Everest's summit the estimated fractional decline in
 O2 max
were ICAO standard conditions to prevail, as some 21%, is greater still than the estimated
fractional decline calculated in the current work for an altitude intermediate between the
final two data points of the Mount Everest simulation study - 8,391 meters (27,530 feet).10
O2 max
were ICAO standard conditions to prevail, as some 21%, is greater still than the estimated
fractional decline calculated in the current work for an altitude intermediate between the
final two data points of the Mount Everest simulation study - 8,391 meters (27,530 feet).10
An independent estimate of the fractional decline in
 O2 max
under ICAO standard conditions, relative to a typical mid-May summit day at Mount Everest,
is provided by applying the relevant entry of Table 3 (summit, May 15): a 515 meter (1,690 foot)
average decline in pressure altitude at the summit relative to its true altitude.
The corresponding increase in atmospheric scale height is 475 meters (1,559 feet).
Multiplication by 4.98 x 10-4 from Equation (C.3d) yields a 24% decline in
O2 max
under ICAO standard conditions, relative to a typical mid-May summit day at Mount Everest,
is provided by applying the relevant entry of Table 3 (summit, May 15): a 515 meter (1,690 foot)
average decline in pressure altitude at the summit relative to its true altitude.
The corresponding increase in atmospheric scale height is 475 meters (1,559 feet).
Multiplication by 4.98 x 10-4 from Equation (C.3d) yields a 24% decline in
 O2 max
were ICAO standard conditions to prevail.
O2 max
were ICAO standard conditions to prevail.
Despite these uncertainties for the exact fractional decline in
 O2 max
under ICAO standard conditions at Mount Everest's summit,
it can be agreed that proper account of temperature,
as manifested in a shift of the atmospheric scale height, plays an essential role
in the physiology of climbing to extreme altitude.
O2 max
under ICAO standard conditions at Mount Everest's summit,
it can be agreed that proper account of temperature,
as manifested in a shift of the atmospheric scale height, plays an essential role
in the physiology of climbing to extreme altitude.
The air pressure experienced at a given true altitude is influenced to a modest degree by the extrapolated sea level temperature. Deviations in pressure altitude due to unusually low or high temperatures are sufficiently large as to be of interest to mountaineers.
Most high altitude ascents occur during the warmer months, and, as such, pressure altitude is lower than true altitude. Mount McKinley is an exception - there, temperatures during the climbing season are only marginally colder (May) or warmer (late June) than the standard atmosphere. Hence pressure altitude is tolerably similar to true altitude. Thereby a given pressure on Mount McKinley is observed at higher altitude elsewhere, all mountains being compared during their respective climbing seasons.
High latitude exerts its influence on air pressure indirectly through colder temperatures. Earth's rotation exerts a minor effect on air pressure via altering the effective value of the acceleration due to gravity. The resulting shift in air pressure is minor.
The warmer, high pressure conditions of ideal summit days provides High Asia mountaineering
expeditions a considerably greater
 O2 max
than is predicted using the ICAO standard atmosphere.
Indeed, climbing Mount Everest without supplemental oxygen is
rendered feasible in large part to this observation. The present work provides a mathematically
rigorous prescription for evaluating this effect.
O2 max
than is predicted using the ICAO standard atmosphere.
Indeed, climbing Mount Everest without supplemental oxygen is
rendered feasible in large part to this observation. The present work provides a mathematically
rigorous prescription for evaluating this effect.
Importantly, the current prescription for pressure altitude may extend outside the realm of mountaineering, applying to studies of long-term adaptation in the indigenous peoples of both the central Andes and Tibet.
1 Valley, S. L.. Handbook of Geophysics and Space Environments McGraw-Hill, New York pp 2-11 to 2-19 (1965).
2 Moore, Terris. The World's Great Mountains: Not the Height You Think. American Alpine Journal pp 109-116 (1968).
3 West, John B.. Prediction of barometric pressures at high altitudes with the use of model atmospheres. Journal of Applied Physiology 81: 4 pp 1850-1854 (October 1996).
4The scale height as realized in the atmosphere differs from that calculated using Equation (8) because of diminishing temperatures with true altitude. Use of sea level temperature for the standard atmosphere as T in Equation (8) yields a scale height of 8,435 meters (27,673 feet). The observed scale height is typically 8,000 meters (26,000 feet), and may be predicted using the more accurate model described in the Section "Modified Hydrostatic Equation".
5The actual expression which replaces gz is g(0)Re /(Re + z). Division of numerator and denominator by Re and expansion of the term 1/(1 + z/Re) yields g(0)z(1 - bz) upon neglect of higher order terms.
6Meteorological data from near Denali Pass, at 5,600 meters (18,400 feet), is available from an automated weather station operated by a Japanese Alpine Club / University of Alaska consortium. It remains to be seen what ridiculously low temperatures it will record this coming 2006-2007 winter.
7The 0.29% fractional shift is obtained by expanding exp(1+x) for x = 0.0029, and retaining terms up to first-order in x.
8 -13.5° C lies in-between the mean January temperatures for Talkeetna and Fairbanks, Alaska - two communities on either side of Denali National Park and Mount McKinley. Extrapolation to sea level and use of Equation (11b) results in the cited equivalent altitude in the summer Himalaya.
9 West, John B.. Human Limits for Hypoxia: The Physiological Challenge of Climbing Mt. Everest. Ann. N.Y. Acad. Sci. 899: pp 15-27 (2000).
10 Sutton, et al.... Operation Everest II: oxygen transport during exercise at extreme simulated altitude. Journal of Applied Physiology 64: 4 pp 1309- (1988).
11The value H used in Equation (C.3d) is that corresponding to the warmer than standard atmosphere of a Mount Everest May summit bid. It is calculated by solving Equations (7c,8) for H, using the observed p = 253 Torr at the summit altitude of z = 8,848 meters. We obtain H = 8,036 meters (26,365 feet).
12The value of z used in Equation (C.3d) is obtained by solving (p* + 47)/760 = exp (-z/H) for z, where p* = PI,O2 / r (O2) and r (02) = 0.22 is the oxygen mole fraction. p* is taken as the average of p* for the two final data points (220.5 Torr). We obtain z = 8,391 meters (27,530 feet).
13A review of the 1981 American Medical Research Expedition to Everest (AMREE) is available on-line as this PDF document.
14 West, John B., et al.... Maximal exercise at extreme altitudes on Mount Everest. Journal of Applied Physiology 55: 3 pp 688-698 (1983).
15 West, John B.. Barometric pressures on Mt. Everest: new data and physiological significance. Journal of Applied Physiology 86: pp 1062-1066 (1999).
Appendix A - Altitude Definitions and Applications
True altitude corresponds to the normal sense of what we think of as elevation above sea level. It differs slightly from geopotential height which is graduated in such a manner that changes in gravitational potential scale linearly in that height measure.
Pressure altitude is that altitude in the standard atmosphere which corresponds to the observed air pressure. When the barometer is reading low, the pressure altitude is higher than the true altitude - and conversely when reading higher than normal.
Pressure altitude is useful in aviation. When flying designated elevations to avoid collision, pilots adjust their cockpit altimeters to the same local airport pressure reading. This enables flight at specific pressure altitudes. In the continental United States all flights above 18,000 feet set altimeters to 29.92 inches of mercury, so allowing separation of levels as well. This value is not arbitrarily chosen - it is the sea level pressure of the standard atmosphere.
Density altitude is that altitude in the standard atmosphere which corresponds to the observed air density. As cold air is heavier than warmer air, the density altitude on a cold day is lower than the true altitude.
Density altitude is critical in flight operations. Wing lift is a function of density altitude, as is engine output power. The length of a runway for takeoff must be long enough to accomodate hot days with their higher density altitudes. Time-to-climb records are performed on very cold winter mornings for increasing performance.
It is the air pressure, and not its density, that forces air into the lungs. Hence in mountaineering pressure altitude is the key quantity forming the subject of this work.
The global atmosphere is constantly in motion. The two principal sources of temperature and pressure variability, and indeed, all of what we refer to as "weather", arise from differential solar heating of the Earth-atmosphere system; and the effect of Earth's rotation. These two phenomena are briefly described.
Strong equatorial solar heating forces air to rise, turn poleward both north and south, and descend around the thirtieth parallels - the Hadley cell. The trade winds return this air equatorward prior to rising again in a complete cycle. Owing to the Coriolis force (see below), trade winds travel west as well as poleward.1
Similar albeit less powerful air currents occur over the polar regions, constituting the Polar cells. Air at the sixtieth parallel is heated to some extent, rises, travels to the poles in the upper troposphere, descends, and then returns to the sixtieth parallel as the west-trending polar easterlies.1 Owing to the Coriolis force these winds have a west component.
The topmost extents of these air currents define the tropopause - in effect, the upper boundary of the troposphere and forming a cap on that atmospheric layer.
These convection cells create semipermanent regions of low and high air pressure at the latitudes of rising or converging air, and hence are of interest here.
A secondary effect dependent on the Hadley and Polar cells is the Ferrel cell of temperate latitudes. Much as a ball bearing is set in motion when placed in-between two larger, rotating bearings, the Ferrel cell exists owing to the Hadley and Polar cells. The Ferrel cell is responsible for the east-trending prevailing westerlies of these latitudes.1
Jet streams are narrow bands of eastward flowing air located between these convection cells - the subtropical jet (near the thirtieth parallels) and the polar jet (near the sixtieth parallels). They result from the large temperature and pressure differences between air in adjacent convection cells; occur near the tropopause; and are, apart from hurricanes and tornadoes, the strongest winds on Earth.
These global currents serve to redistribute heat and, through horizontal pressure and temperature gradients, form the weather patterns commonly seen at mid-latitudes. In contrast, the tropics and polar regions experience less daily variability in weather.
The tropopause height declines from about 15 kilometers (9 miles) at the equator to about 8 kilometers (5 miles) at the poles. This is a purely convective phenomenon and, in particular, does not imply that the atmospheric scale height varies in similar fashion.
The Coriolis effect is an apparent deflection of a moving object in a rotating reference frame, e.g. Earth's surface. The deflection is fictitious: to an observer in a non-rotating (i.e., inertial reference frame), there is no deflection. However to an observer fixed to the rotating reference frame, such as Earth's surface, moving objects appear to be deflected from straight-line paths.
Consider a parcel of air traveling due north from the equator. To a distant observer fixed in space the parcel also contains a large eastern component equal in magnitude to the speed of rotation at the equator - roughly 1,670 kilometers per hour (1,030 miles per hour). As the parcel crosses parallels of latitude the underlying surface is traveling slower than at the equator. Hence the air parcel will, in the absence of any external force, assume an easterly component to it's motion relative to the underlying surface.
However to an Earth-based, co-rotating observer a ficitious force appears to be pushing the air parcel east. This is the Coriolis effect.
The Coriolis effect caused by Earth's rotation is responsible for the direction of rotation of weather patterns. The effect deflects objects moving along Earth's surface to the right in the North Hemisphere and to the left in the South Hemisphere. Thus winds around the center of a cyclone rotate counterclockwise in the North Hemisphere and clockwise in the South Hemisphere.
Global atmospheric convection cells are altered by the Coriolis effect. Equator-bound trade winds (see last section) assume a westerly component, as do the subpolar easterlies descending from the poles. Similary, mid-latitude prevailing westerlies assume an easterly component.
Consider the combined effects of pressure gradients and the Coriolis effect associated with a low pressure region. Due to the lower pressure, air will flow into such a region, and, in the absence of Earth's rotation, would assume straight paths. However the Coriolis force deflects these paths perpendicular to the direction of motion. There results an equilibrium of pressure and Coriolis-generated motions wherein a circular pattern is established - a cyclonic flow.
Cyclonic flow is one instance of the more general geostrophic balance wherein air flows along isobars. On a non-rotating planet the air would flow along the straightest possible line, quickly zeroing pressure gradients.
In the Northern Hemisphere air motion around a low-pressure center is counterclockwise. High pressure creates an anticyclone with clockwise motion. In the Southern Hemisphere these senses of rotation are reversed.
The Coriolis force is zero at the equator, and cyclones cannot form there. The Coriolis force is greatest in mid-latitudes.
The interplay of Coriolis forces and global convection currents results in deviations of sea level pressure which, in turn, effect the calculation of pressure altitude.
1 In a most unfortunate choice of nomenclature, in meteorology wind directions are described by the direction of origin, i.e. a wind traveling south is a "northerly" wind. This runs counter to both intuition and all rest of mathematics and science wherein the components of a vector are based on the final coordinates less the initial coordinates.
 O2 max
Upon Atmospheric Scale Height
O2 max
Upon Atmospheric Scale HeightPI,O2 is a simple, exponentially decaying
function of pressure altitude.1
In contrast, 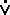 O2 max depends upon several physiological variables;
and is, even today, not completely understood.
O2 max depends upon several physiological variables;
and is, even today, not completely understood.
These variables include level of cardiovascular fitness, degree of altitude acclimatization,
extent of hyperventilation, blood chemistry (especially pH shift), genetic heritage, individual size,
and, of course, the ambient pressure.
Individual size is trivially eliminated by discussing maximal oxygen consumption per unit mass,
 O2 max.
O2 max.
However the remaining physiological variables are correlated, making it untenable
that a model wherein  O2 max
depends just linearly on these variables is viable,
O2 max
depends just linearly on these variables is viable,
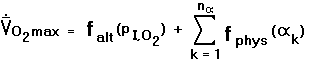 |
(C.1a) |
In Equation (C.1a) { k}
is the set of physiological variables which determine maximal oxygen consumption rate
k}
is the set of physiological variables which determine maximal oxygen consumption rate
Nevertheless it must be agreed that the overwhelmingly critical determinant of
 O2 max
is altitude and its direct effect upon PI,O2:
no superfit, fully acclimatized mountain native at Mount Everest's South Col can possibly
compete with a sedendary lowlander at sea level.
O2 max
is altitude and its direct effect upon PI,O2:
no superfit, fully acclimatized mountain native at Mount Everest's South Col can possibly
compete with a sedendary lowlander at sea level.
We thus consider factoring Equation (C.1a) into a pair of terms,
 |
(C.1b) |
In Equation (C.1b) falt(o) (PI,O2)
is the explicit dependence of
 O2 max
upon inspired oxygen partial pressure for a predefined, baseline physiologic state
(denoted by the "o" superscript); and fphys
(
O2 max
upon inspired oxygen partial pressure for a predefined, baseline physiologic state
(denoted by the "o" superscript); and fphys
(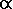 1,
1,
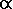 2,
2,
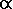 3, ....)
represents the collective linear and nonlinear variations of
3, ....)
represents the collective linear and nonlinear variations of
 O2 max
wrought by the aforementioned physiological factors.
The baseline physiologic state may be that of a sedentary, unacclimatized individual residing at sea level.
O2 max
wrought by the aforementioned physiological factors.
The baseline physiologic state may be that of a sedentary, unacclimatized individual residing at sea level.
One demonstrates that Equation (C.1b) is an inappropriate factorization as follows.
A hypothetical, sedentary, and unacclimatized individual is unable to perform useful physical work
at the summit of Mount Everest; and, indeed, would rapidly lose consciousness.
His  O2 max,
although nonzero, does not meet that minimal amount required to maintain body functions even at complete rest.
O2 max,
although nonzero, does not meet that minimal amount required to maintain body functions even at complete rest.
A very fit and fully acclimatized climber is able to perform useful physical work in this environment,
as demonstrated by successful ascents of Mount Everest without supplemental oxygen.
Consequently the ratio of their respective  O2 max on the left side of Equation (C.1b) differs markedly from unity;
and by inspection, this ratio must be entirely due to the second factor on the right hand side since
the first factor depends but on altitude.
O2 max on the left side of Equation (C.1b) differs markedly from unity;
and by inspection, this ratio must be entirely due to the second factor on the right hand side since
the first factor depends but on altitude.
At sea level these two individuals also differ in  O2 max, and, again, the ratio of their respective
O2 max, and, again, the ratio of their respective
 O2 max values
must equal the ratio of their respective second factors on the right hand side of Equation (C.1b).
This maximum oxygen consumption ratio is roughly 1.5 at sea level, once normalized
to account for individual size variability.2
As the second factor on the right hand side of Equation (C.1b) is independent of altitude,
the same ratio must apply as well at Mount Everest's summit.
O2 max values
must equal the ratio of their respective second factors on the right hand side of Equation (C.1b).
This maximum oxygen consumption ratio is roughly 1.5 at sea level, once normalized
to account for individual size variability.2
As the second factor on the right hand side of Equation (C.1b) is independent of altitude,
the same ratio must apply as well at Mount Everest's summit.
A contradiction thus results since the acclimatized climber is certainly capable of achieving more than
1.5 times that  O2 max
required to simply maintain consciousness: he has, after all, walked uphill to achieve the summit!
O2 max
required to simply maintain consciousness: he has, after all, walked uphill to achieve the summit!
We conclude that  O2 max
cannot be simply factored into separate altitude and physiological components:
a more general prescription is required.
O2 max
cannot be simply factored into separate altitude and physiological components:
a more general prescription is required.
Equation (C.1b) is replaced by
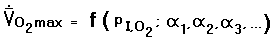 |
(C.1c) |
where
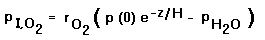 |
(C.2) |
relates the inspired oxygen partial pressure to barometric pressure under the simplifying approximation of Equation (7c).
Equation (C.1c) contains both linear and nonlinear terms in the underlying variables.
The nonlinear terms represent the interdependencies of variables
upon one another; and, as demonstrated above, are required for internal consistency.
Equation (C.1c) is the most general statement possible about the relationships determining
 O2 max,
having made no assumptions whatsoever in its formulation.
O2 max,
having made no assumptions whatsoever in its formulation.
Consider the dependence of
 O2 max
upon the air column temperature profile. Equation (8) relates absolute temperature T to the
atmospheric scale height H. Differentiating Equation (C.1c) with respect to H,
O2 max
upon the air column temperature profile. Equation (8) relates absolute temperature T to the
atmospheric scale height H. Differentiating Equation (C.1c) with respect to H,
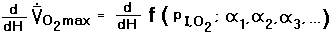 |
(C.3a) |
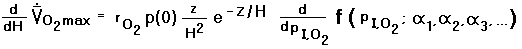 |
(C.3b) |
Equation (C.2) is used for the derivative of PI,O2 with respect to H.
Explicitly writing the terms in f (PI,O2;
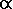 1,
1,
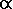 2,
2,
 3, ...),
3, ...),
 |
(C.4) |
In Equation (C.4) f(0) (PI,O2) is the explicit dependence of
 O2 max
upon altitude; the set of {f(k) (
O2 max
upon altitude; the set of {f(k) (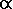 k)}
is the altitude-independent dependence of
k)}
is the altitude-independent dependence of
 O2 max
upon physiological variables; and the set of {f(0,k)
(PI,O2,
O2 max
upon physiological variables; and the set of {f(0,k)
(PI,O2, 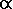 k)}
are the cross-terms, of all orders, that are the nonlinear dependencies of
k)}
are the cross-terms, of all orders, that are the nonlinear dependencies of
 O2 max
upon both altitude and physiological variables. Recall that these nonlinear terms render
Equation (C.1b) inadequate.
O2 max
upon both altitude and physiological variables. Recall that these nonlinear terms render
Equation (C.1b) inadequate.
Substituting Equation (C.4) into Equation (C.3b),
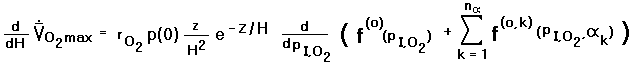 |
(C.3c) |
and
 |
(C.3d) |
The fractional change in maximal oxygen consumption with atmospheric scale height
is most elucidating when discussing extreme altitudes. Thus in Equation (C.3d) we have divided
by  O2 max.
O2 max.
It is quite difficult, if not impossible to experimentally measure the individual
terms on the right hand side of Equation (C.3d). One can, however, measure
 O2 max
and then, noting Equations (C.1c) and its expansion as Equation (C.4),
determine the derivative on the right hand side of Equation (C.3d) numerically
from the differences in
O2 max
and then, noting Equations (C.1c) and its expansion as Equation (C.4),
determine the derivative on the right hand side of Equation (C.3d) numerically
from the differences in  O2 max at adjacent data points.3
In so doing one has lost the knowledge of how, as f(0) (PI,O2),
maximal oxygen consumption is directly effected by altitude.
O2 max at adjacent data points.3
In so doing one has lost the knowledge of how, as f(0) (PI,O2),
maximal oxygen consumption is directly effected by altitude.
Furthermore, the derivatives so obtained will be correct only for the specific set
of physiological variables employed in the observations. Thus if the maximal oxygen
consumption of fit, acclimatized individuals is measured, and then differences in these
consumption rates are taken across a range of PI,O2 values,
the resulting calculated dependence of  O2 max upon atmospheric scale height H (c.f.
Equation (C.3d)), will only be applicable to that cohort.
The entire space of physiological variables
{
O2 max upon atmospheric scale height H (c.f.
Equation (C.3d)), will only be applicable to that cohort.
The entire space of physiological variables
{ k}
must be sampled to assess how air temperature, via the scale height,
effects physiological performance for all individuals.
k}
must be sampled to assess how air temperature, via the scale height,
effects physiological performance for all individuals.
Equation (C.3d) contains a factor of
z exp (-z/H) / H2 pre-multiplying the derivative.
Differentiation of this expression by z yields a zero derivative at z = H,
i.e. at the atmospheric scale height this factor is maximal.
Hence at Mount Everest's South Col, wherein z is roughly the scale height,
and everything else being equal, the fractional dependence of
 O2 max
upon air temperature change is maximized.
O2 max
upon air temperature change is maximized.
1The vapor pressure of water at 37° C is 47 Torr. It is subtracted from the barometric pressure after applying the altitude-dependent exponential factor. Thus PI,O2 = r (O2) [p(0)exp (-z/H) - p(H2O)], where r (O2) is the oxygen mole fraction; and p(H2O) is the water vapor pressure. Numerically, PI,O2 = 0.21 [760 exp (-z/H) - 47] (in Torrs).
2 Ferretti, G., et al.... The decrease of maximal oxygen consumption during hypoxia in man: a mirror image of the oxygen equilibrium curve. Journal of Physiology 498: 1 pp 231-237 (1997).
3The derivatives of all terms in the first sum of Equation (C.4) with respect to PI,O2 vanish. The remaining terms correspond to the required terms on the right hand side of Equation (C.3d).