Cache Placement Analysis

Cache Placement Analysis ^*

^* by Adam Helman

Introduction

Strategic placement of supplies is an essential part of many outdoor activities ranging from simple dayhikes in hot weather to multiday expeditions. This study analyzes how the number and location of caches effects the additional effort required to transport the corresponding supplies.

Denote the mass of a climber by M, and the mass of his supplies by m. For a day-long effort m << M, and it is valid to derive equations assuming that the energy for carrying mass m, or some fraction thereof, over a unit distance is proportional to simply m .

For a multiday outing this linear approximation is not valid; and one must account for the combined mass, M + m, in deriving equations for how much energy is consumed. Indeed, crossing Antarctica on skis while manhauling a heavy sled has m >> M. The effort for traveling a unit distance is initially quite large; and gradually wanes as m declines.

In the current note only the case of m << M is considered. The main application corresponds to a day-long hike, or climb, with food and water consumed enroute. On a hot day it then becomes reasonable to cache water, the amount stored then consumed during the descent. Henceforth the word "water" shall represent the summed total of all consumables. For a day-long affair one would not normally cache more than water anyway.

Several factors determine how much water is consumed while maintaining fluid hydration. These include, but are not limited to, temperature, relative humidity, sun or shade, clouds or clear sky, clothing worn, and body type. It is impossible to derive an analytical model accounting for all these factors. Therefore the current aim is not to estimate how much water is required. Rather, given an assumed water requirement, where are caches to be placed so as to lessen or even minimize the effort of carrying water as summed over the entire day.

This study was conceived the day prior to climbing the largest prominence of Sonora state in Mexico on April 12, 2010. Sufficient motivation was provided by the perceived need for carrying six quarts of water per person.

Definitions

The following model parameters are used.

n - Number of caches.

N - Number of caches plus one.

N simplifies the derivation of equations compared with using n itself.
When there are no caches N = 1. When there is one intermediate cache N = 2.
Hence N is the number of sections in an ascent from trailhead to the summit.

f - Fraction of physical effort required for the ascent. If the hike is generally flat then f = 1/2.
If a true climb, f > 1/2. I have empirically found f = 2/3 is a good general rule of thumb.
For an "inverse climb" (e.g. Bright Angel Trail of the Grand Canyon) f < 1/2.

r - Fraction of water required for the ascent. On a cold and/or completely cloudy day
r should equal f. On a sunny day with rising afternoon temperatures I have empirically
found r = 1/2 is a good general rule of thumb.

Parameter r accounts for temperature changes as shown by example.
When f = 2/3, only 1/3 of the effort is consumed on descent. Hence with r = 1/2,
twice as much water is drunk per unit energy expended on the descent compared
with the ascent as (2/3 / 1/2) / (1/3 / 1/2) = 2.

p - Fraction of water drunk at each cache relative to the total amount required
for reaching the next cache. When p = 0 water is assumed drunk only along the route.
When p = 1 the same water is completely consumed prior to setting-out.

People differ as to how much water is consumed while at a rest stop.
Parameter p accounts for this observation.

To simplify the derivations we define the energy required to carry a constant mass m to the summit and back as 1.0 unit. This energy is beyond that required to carry one's self and nonconsumable items. We also set m = 1.0, and define as unit distance and elevation change the route from trailhead to summit.

These normalizations result in energy formulae that are fractions of the energy for the theoretical case described above. Clearly, all real scenarios yield energies less than 1.0 since the water's mass declines throughout the day.

Later we have use for these additional parameters.

c - Fraction of the total energy for the {n = 0, p = 0} case required for placing and retrieving one cache.
h - Fraction of elevation gained and/or distance traveled upon reaching a cache.

n Equally Spaced Caches

Consider the mean mass of water carried from the trailhead to the first of several caches. The amount of water consumed prior to arrival at cache 1 is N^-1 r. Of this amount, a fraction p was consumed at the trailhead and fraction 1 - p while in-transit.

Recalling that m = 1 initially, the mass on departing the trailhead is thus 1 - N^-1 rp. Futhermore, the mass on arriving at cache 1 is 1 - N^-1 r. Hence the mean mass for this route section is their average as 1 - (1/2) N^-1 r (1 + p).

The quantity cached is the amount required to descend from cache 1 to the trailhead, namely, N^-1 (1 - r). The amount consumed at cache 1 is N^-1 rp. Subtracting these two quantities from the cache 1 arrival mass, the mass on cache 1 departure is, after some rearrangement, 1 - N^-1 (1 + rp).

Subtracting from this quantity one-half the amount consumed to reach cache 2, the mean mass for traveling from cache 1 to cache 2 is 1 - N^-1 [1 + (1/2) r (1 + p)].

Repeating this theme, the mean mass while traveling from cache 2 to cache 3 is 1 - N^-1 [2 + (1/2) r (1 + p)]; and, more generally, from cache i to cache i + 1, 1 - N^-1 [i + (1/2) r (1 + p)].

Adding the N mean masses, recalling that n = N - 1, and simplifying,

Multiplying by the fractional energy-distance f N^-1 for a single section, the normalized energy for reaching the summit is

E (ascent) = (f/2) [1 + N^-1 (1 - r (1 + p)) ]. [1]

Equations for the descent are simpler to derive. One arrives at the summit with mass N^-1 (1 - r), rationalized as the amount of water needed for descent to the highest cache. Here, N^-1 is the normalized distance (and/or elevation gain); and 1 - r is the rate of consumption.

The mass not immediately consumed is the initial mass carried on descending to the next cache, N^-1 (1 - r) (1 - p). On arriving at the next cache the amount carried is zero since all water for the next segment is at the cache. Hence the mean mass carried on descent, for all segments, is always (1/2) N^-1 (1 - r) (1 - p).

Summing over N segments, (1/2) (1 - r) (1 - p). Multiplying by the fractional energy-distance (1 - f) N^-1 for a single section on the descent, the normalized energy for descent to the trailhead is

E (descent) = (1/2) (1 -f ) (1 - r) (1 - p). [2]

Consider now the most energy-intensive practical case, one wherein there are no caches (n = 0, N = 1); and where no water is consumed at both trailhead and summit (p = 0). The ascent energy is given by Eq.[1] as (f/2) (2 - r) = f (1 - r/2). From Eq.[2] the descent energy is (1/2) (1 -f ) (1 - r). Adding and simplifying, the normalized energy for this special case is

E (total) = (1/2) (1 + f - r). [3]

Adding Eq.[1] and Eq.[2], dividing by Eq.[3], and cancelling the factors of 1/2, the normalized total energy (relative to the {n = 0, p = 0} case) is

E (total) = ( f + N^-1 [f - fr (1 + p) + (1 - f) (1 - r) (1 - p)] ) / (1 + f - r). [4]

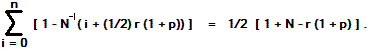
Examples

Consider cases wherein {f = 2/3, r = 1/2} while both n and p assume different values.
Eq.[4] simplifies to E (total) = 4/7 + (3/7) N^-1 (1 - p).

n = 0 and p = 0. E (total) = 1.0, as expected by the normalization.

n = 1 and p = 0. E (total) = 11/14, a saving in energy of 21.4% by placing one cache.

n = 2 and p = 0. E (total) = 5/7, an overall saving of 28.6% by placing two caches.
Note how the second cache creates less energy saving than the initial cache.

n = 3 and p = 0. E (total) = 19/28, an overall saving of 32.1%.

Infinite caches. E (total) = 4/7, a lowering of total energy by 42.9%.

Clearly it is absurd to place an infinite number of caches. Later an energy penalty factor is applied for cache placements that results in a finite minimum-energy cache count.

n = 0 and p = 1. E (total) = 4/7.

The energy saved by simply drinking all water for the ascent while still at the trailhead; and all water for the descent while at the summit equals the amount saved by emplacing an infinite number of caches while drinking all water while in-motion.

By inspection, the term (1 - p) of E (total) = 4/7 + (3/7) N^-1 (1 - p) results in the same total energy, independent of cache count, when p = 1. This is not a general result, and arises from the terms f - fr (1 + p) in the numerator of Eq.[4]. Setting these terms equal to zero, the required condition is that r (1 + p) = 1.0 - a condition met when, as in these examples, r = 1/2 and p = 1.

It is risky to drink all of one's water at the trailhead, for the ascent, even though it lowers the energy cost: one could get lost. Furthermore, much of that water, if drunk all-at-once in large quantity, will simply pass nike shox experience through the body and be urinated before it has a chance to be properly utilized.

The best strategy from a practical standpoint, may be to space caches such that the amount drunk at each cache will be completely utilized during travel - and yet one should begin to feel "thirsty" JUST upon reaching the next cache - no sooner. How such a spacing of caches compares with the optimal-energy cache count of the next section is currently unknown.

Energy to Create Caches

We address the issue of an infinite cache count minimizing the energy of carrying water. Using the definition of c, the energy of emplacing and retrieving one cache is, from Eq.[3], just (1/2) c (1 + f - r). The numerator of Eq.[4] takes this additional term,

E (total) = ( f + N^-1 [f - fr (1 + p) + (1 - f) (1 - r) (1 - p)] + c (N -1) ) / (1 + f - r). [4']

In deriving Eq.[4'] we recall there are n = N - 1 caches; and factors of 1/2 have been cancelled.

Consider again cases with {f = 2/3, r = 1/2}. Eq.[4'] then simplifies to E (total) = 4/7 + (3/7) N^-1 (1 - p) + (N - 1) c.

For p = 0 we have E (total) = 4/7 + (3/7) N^-1 + (N - 1) c. The total energy will initially decline for small N, and then be overwhelmed by the term (N - 1) c for large N.

Considering E (total) to be a continuous function of N, differentiation yields d E (total) / d N = - (3/7) N² + c. Setting this expression to zero, N = (3 / 7c)^1/2 at the "break-even point" in cache count.

Let c = 0.01, corresponding to 5 minutes in an 8 hour total effort. Substitution into the very last formula (in boldface) yields N = 10 (3/7)^1/2 = 6.5, i.e. 5.5 caches yield the minimum energy for {f = 2/3, r = 1/2, p = 0}.

For p = 1 it makes no sense to have any caches: by inspection, for the case {f = 2/3, r = 1/2}, since from Eq.[4] E (total) is independent of N; leaving just the term in c to raise the energy with rising cache count.

Minimum Energy Cache Placement - One Cache

Consider a generalization of the single cache case. We wish to find the location of that cache so as to minimize the total additional energy spent by carrying consumables.

We use a derivation completely analogous to that in Section "n Equally Spaced Caches", albeit with parameter h being accounted for throughout.

The mean mass carried from the trailhead to the cache is m₁ = 1 - (1/2) hr (1 + p).
The mean mass carried from the cache to the summit is m₂ = 1 - h - (1/2) [r (1 - h)(1 + p)] .

The ascent energy is thus

E (ascent) = f ( h m₁ + (1 - h) m₂) [5a]
= f (h - (1/2)h²r (1 + p) + (1 - h²)[1 - (1/2)r (1 + p)] ). [5b]

The mean mass carried from the summit down to the cache is m₃ = (1/2) (1 - h) (1 - r) (1 - p).
The mean mass carried from the cache down to the trailhead is m₄ = (1/2) h (1 - r) (1 - p).

The descent energy is thus

E (descent) = (1 - f) ((1 - h) m₃ + h m₄) [6a]
= (1/2) (1 - f) (1 - r) (1 - p) (1 - 2h + 2h²). [6b]

To obtain the optimal cache location we minimize the summed ascent and descent energy for any triple {f, r, p} by taking the derivative of the summed energy with respect to h, setting it to zero, and solving for h.

d E (total) / dh = (1 - f) (1 - r) (1 - p) (2h - 1) = 0 [7]

By inspection the desired solution is h = 1/2, i.e. a cache placed halfway between the trailhead and summit minimizes the total energy for carrying consumables for any given triple {f, r, p}. This mundane and admittedly uninteresting result can also be derived by symmetry-based arguments.

Minimum Energy Cache Placement - Two Caches

Consider a generalization of the two cache case. We desire the locations of both caches so as to minimize the total additional energy spent by carrying consumables.

We use a derivation analogous to the previous Section. Parameter h₁ is the fractional distance and/or elevation gain beyond the trailhead of the first cache. Similarly, parameter h₂ is the fractional distance and/or elevation loss from the summit to the second cache.

The mean mass carried from the trailhead to the first cache is m₁ = 1 - (1/2) h₁ r (1 + p).
The mean mass carried from the first to the second cache is m₂ = 1 - h₁ - (1/2) r (1 + p) (1 - h₁ - h₂).
The mean mass carried from the second cache to the summit is m₃ = h₂ - (1/2) h₂ r (1 + p).

Thus

E (ascent) = f (1 - h₁ - h₂ + h₁² + h₁ h₂ + h₂² - (1/2) r (1 + p) [h₁² + h₂² + h₃²] ) [8]

where h₃ = 1 - h₁ - h₂.

The mean mass carried from the summit down to the higher cache is m₄ = (1/2) h₂ (1 - r) (1 - p).
The mean mass carried from the higher cache down to the lower cache is m₅ = (1/2) (1 - h₁ - h₂) (1 - r) (1 - p).
The mean mass carried from the lower cache down to the trailhead is m₆ = (1/2) h₁ (1 - r) (1 - p).

Thus

E (descent) = (1/2) (1 - f) (1 - r) (1 - p) [h₁² + h₂² + h₃²]. [9]

To obtain the optimal pair of cache locations we minimize the summed ascent and descent energy for any triple {f, r, p} by taking the partial derivatives of the summed energy with respect to h₁ and h₂; set them both to zero; and then solve the resulting pair of simultaneous equations that are linear in h₁ and h₂.

d E (total) / dh₁ = [ f (1 - r[1 + p]) + (1 - f) (1 - r) (1 - p) ] x (2h₁ + h₂ - 1) = 0 [10]

and

d E (total) / dh₂ = [ f (1 - r[1 + p]) + (1 - f) (1 - r) (1 - p) ] x (2h₂ + h₁ - 1) = 0 [11]

By inspection the desired solution is h₁ = h₂ = 1/3, i.e. two caches evenly-spaced between the trailhead and summit minimizes the total energy for carrying consumables for any given triple {f, r, p}.

graphic home page

text-only home page